python機器學習入門到實踐—day01(筆記)
主要內容:
1.在python中使用均值、中位數和眾數
(1)使用 NumPy 包計算均值
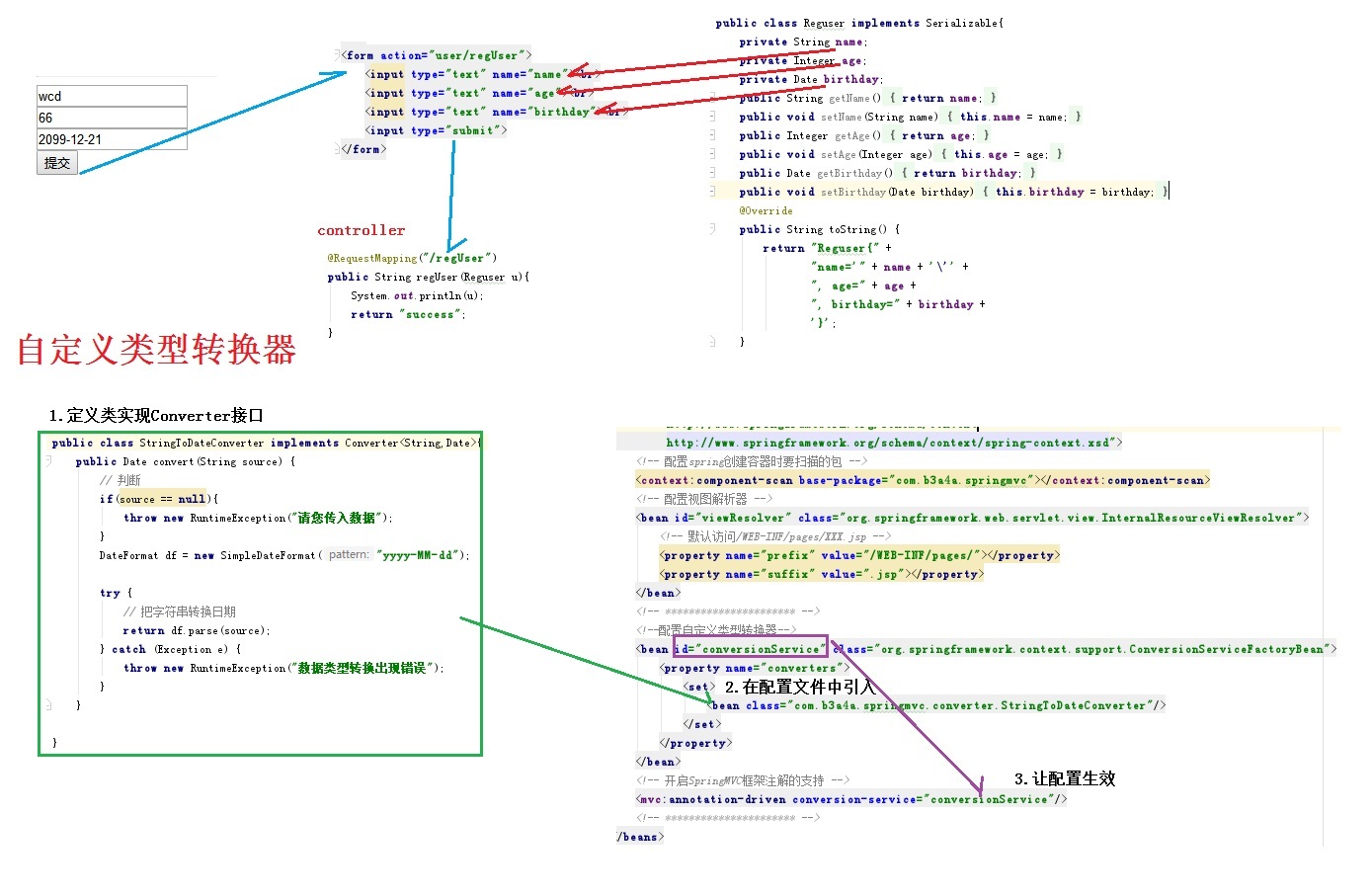
NumPy 可以非常容易地計算均值、中位數和眾數。我們直接使用 import numpy as np,這意味著導入以后可以使用 np 作為 numpy的簡寫。使用 np.random.normal 函數創建一個名為 incomes 的數值列表。
np.random.normal 函數的 3 個參數的意義是,創建的數據集中在 27 000 附近,標準差為15 000,列表中有 10 000 個數據點。
import numpy as np
incomes=np.random.normal(27000,15000,10000)
#求平均值
print(np.mean(incomes)) #26715.907596870416
使用 matplotlib 進行數據可視化
import numpy as np
import matplotlib.pyplot as plt
incomes=np.random.normal(27000,15000,10000)
#求平均值
print(np.mean(incomes)) #26715.907596870416
plt.hist(incomes,50)
plt.show()
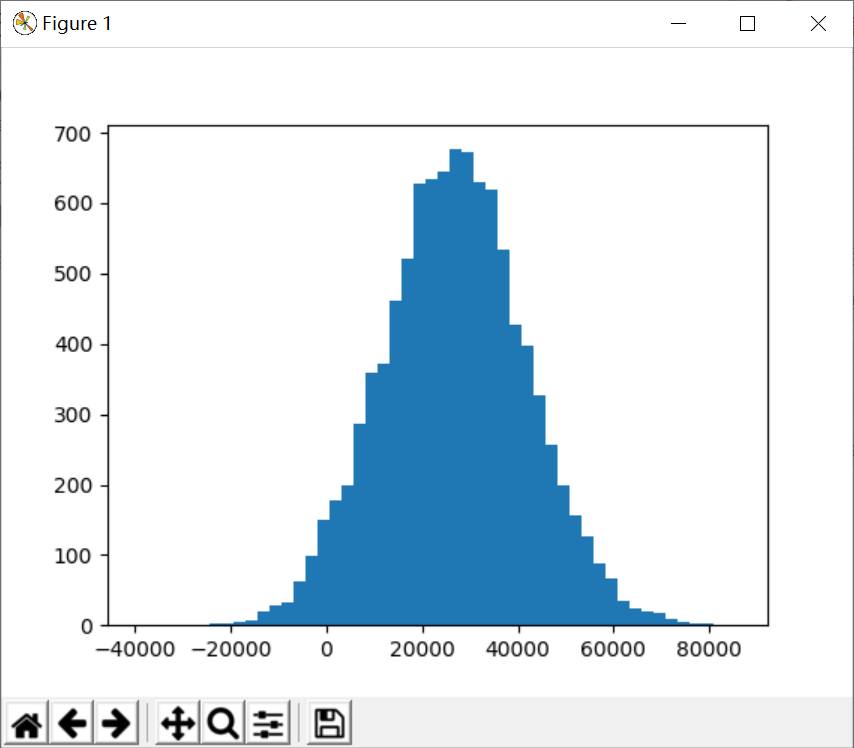
(2)使用 NumPy 包計算中位數
import numpy as np
incomes=np.random.normal(27000,15000,10000)
x=np.median(incomes)
print(x) #27082.117137121946
(3)使用 SciPy 包計算眾數
將生成 500 個隨機整數,范圍從 18 到 90。這段代碼中,眾數為 68,這是數組中出現次數最多的數,它出現了 15 次。
import numpy as np
from scipy import stats
ages=np.random.randint(18,90,size=500)
x=stats.mode(ages)
print(x) #ModeResult(mode=array([68]), count=array([15]))
2.標準差和方差
(1)總體方差:總體方差通常表示為西格瑪的平方(σ2),西格瑪(σ)是標準差。用每個數據點 X 減去均值 μ,對差進行平方,再進行求和,然后除以數據點的個數 N,就可以算出總體方差。可以用下面的公式表示:
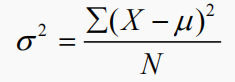
? X 表示每個數據點;
? μ 表示均值;
? N 表示數據點的個數。
(2)樣本方差:樣本方差用 S2表示,公式如下:
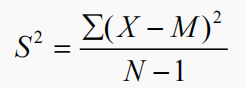
? X 表示每個數據點;
? M 表示均值;
? N – 1 表示數據點的個數減 1。
(3)使用 std 來計算標準差。
import numpy as np
incomes=np.random.normal(100,20,500)
x=incomes.std()
print(x) #20.095087108660174
(4)使用 var 函數計算方差。
import numpy as np
incomes=np.random.normal(100,20,500)
x=incomes.var()
print(x) #402.36828829119344
3.概率密度函數和概率質量函數
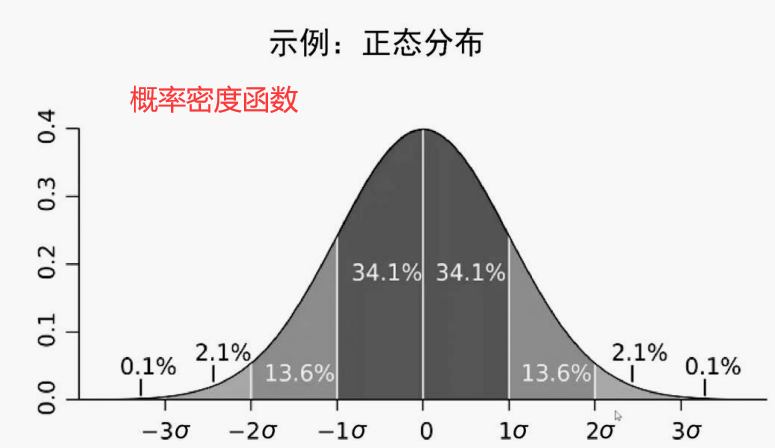
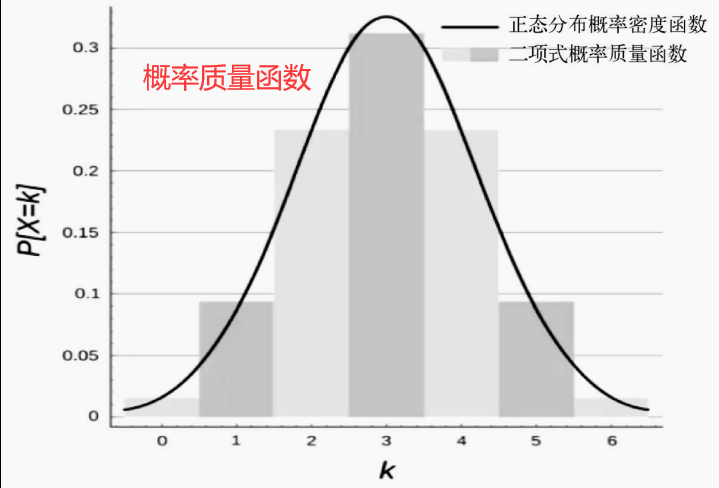
概率密度函數實際上表示的是一個特定范圍的值發生的概率,這就是概率密度函數的意義。如果你處理的是離散型數據,那么其處理方法會和連續型數據有所不同,這時要使用概率質
量函數,概率質量函數就是離散型數據發生概率的具體表示,它看上去很像直方圖,實際上也就是個直方圖。概率密度函數是一條曲線,描述了某個范圍內的連續型數據出現的概率。概率質量函數是某個離散值出現在數據集中的概率。
4.各種類型的數據分布
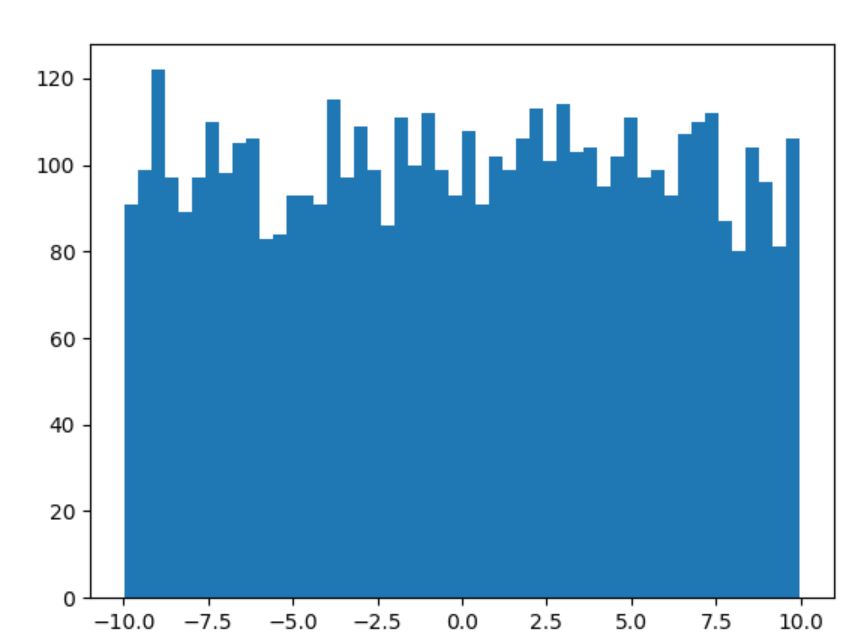
(1)均勻分布:均勻分布意味著在給定范圍內,數值出現的概率是一條水平固定的直線。使用 NumPy 的 random.uniform 函數,可以創建一個均勻分布。代碼的含義是,生成一組服從均勻分布的隨機值,取值范圍從–10 到 10,數量為 5000 個。
import numpy as np
import matplotlib.pyplot as plt
values=np.random.uniform(-10,10,5000)
plt.hist(values,50)
plt.show()
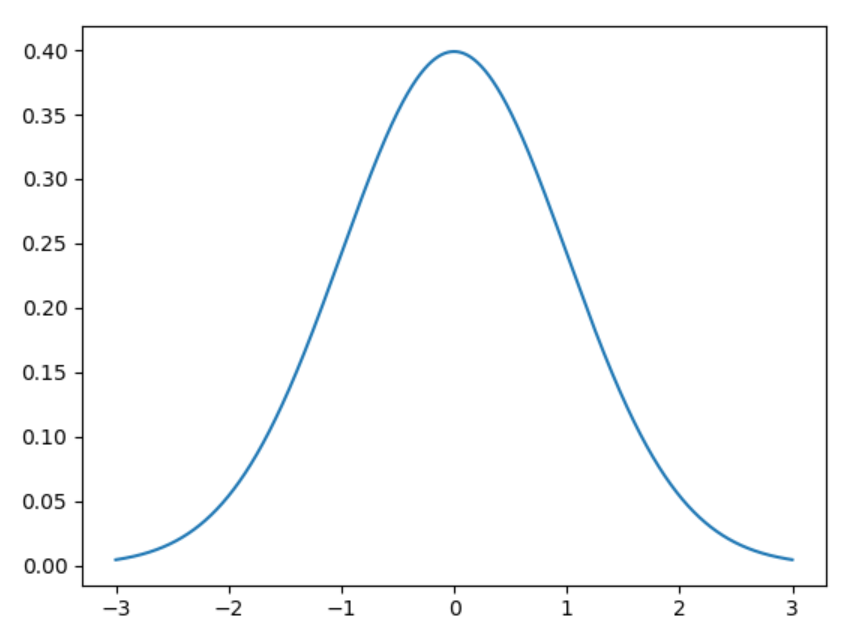
(2)正態分布或高斯分布:正態分布又稱高斯分布,Python 的 scipy.stats.norm 包有一個 pdf(probability density function)函數,可以對其進行可視化。
使用函數 arange 創建了一個列表 x 用來繪制圖形,列表的值在–3 和 3 之間,增量為 0.001。在圖形中,x 軸使用的就是這些列表值,y 軸是一個正態分布函數 norm.pdf,也就是 x 值對應的正態分布概率密度函數值。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
x=np.arange(-3,3,0.001)
#norm.pdf(x)正態分布函數或概率密度函數
plt.plot(x,norm.pdf(x))
plt.show()
(3)指數概率分布與指數定律:另一個常見的分布函數是指數概率分布函數,其函數值以指數方式下降。說起指數下降,是指一條曲線上在 0 附近的值發生的概率很高,但當遠離 0 時,值會急速下降。自然界中很多事物都符合這種情況。在 Python 中,scipy.stats 包中既有 norm.pdf 函數,也有 expon.pdf 函數,后者就是Python 中的指數概率分布函數。和正態分布的語法一樣,可以在代碼中使用指數分布:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon #指數概率函數
x=np.arange(0,10,0.001)
plt.plot(x,expon.pdf(x))
plt.show()
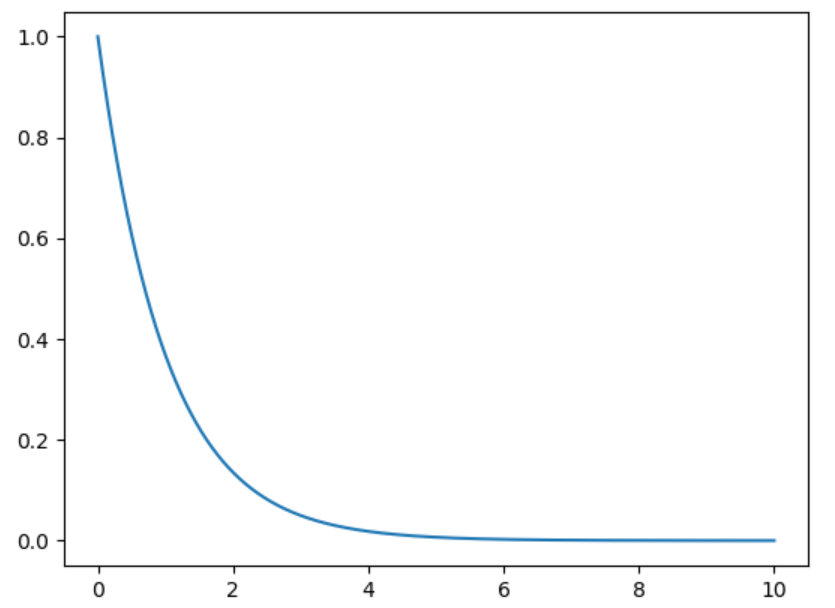
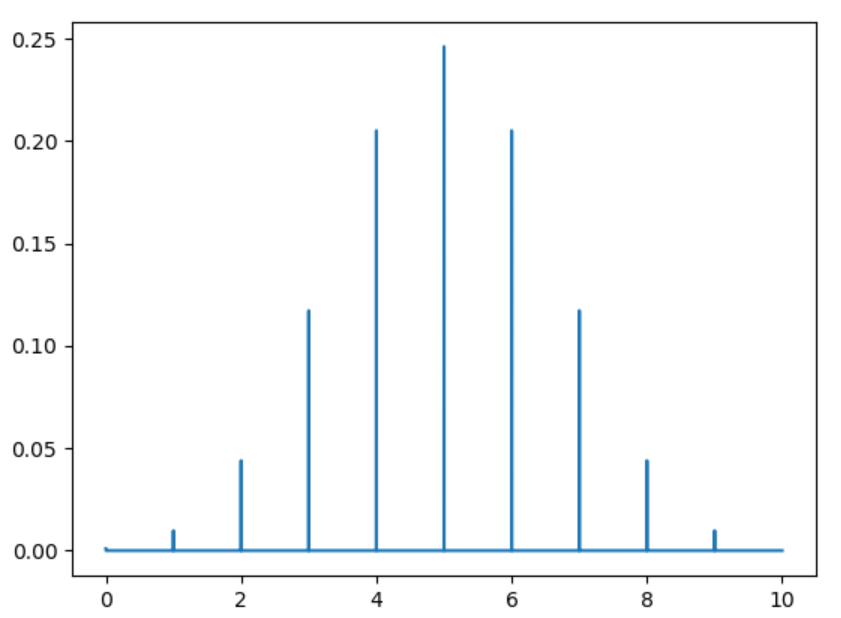
(4)二項式概率質量函數:
我們也可以對概率質量函數進行可視化,比如二項式概率質量函數。這次不使用 expon 或 norm,而是使用 binom。注意:概率質量函數處理的是離散數據。 binom.pmf 函數中,我們使用兩個參數 n 和 p 來設定數據的形狀。在這個代碼中,n 和 p 分別是 10 和 0.5。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
x=np.arange(0,10,0.001)
plt.plot(x,binom.pmf(x,10,0.5))
plt.show()
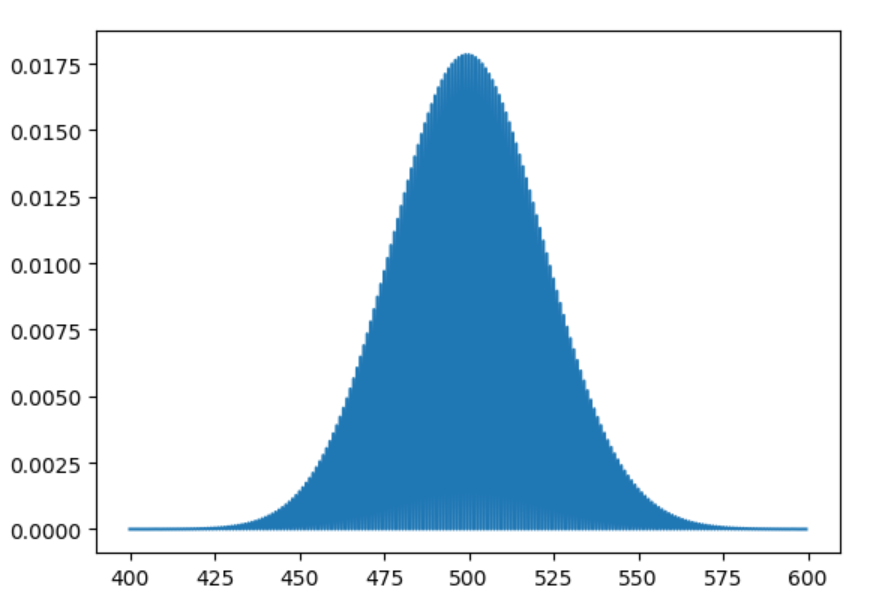
(5)泊松概率質量函數:
這是個比較特殊的分布,與正態分布非常像,但有一點不同。如果你知道了在給定時間段內某個事情發生的平均次數,那么就可以使用泊松概率質量函數來預測未來某個時段這個事情發生另一個次數的概率。
在這個代碼中,平均數 mu 是 500。創建一個列表 x,值從 400 到 600,間隔為 0.5。使用poisson.pmf 函數繪制這些數據。可以使用這個圖形找出不是 500 的某個值發生的概率。
某一天有 550 個訪客的概率是 0.002,即 0.2%。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
x=np.arange(400,600,0.5)
mu=500
plt.plot(x,poisson.pmf(x,mu))
plt.show()
5.百分位數和矩
什么是百分位數?一般來說,如果將數據集中所有數據排好順序,那么第 x 個百分位數就是這樣一個點:數據集中 x%的數據都小于它。例如:設我們在討論美國所有人的收入,并對收入進行了排序,那么第99 個百分位數就是 99%的美國人的收入都小于它的那個數。
(1) 四分位數:
在一個分布中,常用的百分位數又稱四分位數。第一個四分位數(Q1)和第三個四分位數(Q3)
之間包含的點正好是 50%的數據點,所以中位數左側有 25%的數據點,右側也有 25%的數據點。本例中的中位數恰好與均值非常接近。例如,四分位距(InterQuartile Range,IQR)就是分布中間包含 50%數據的那塊面積。
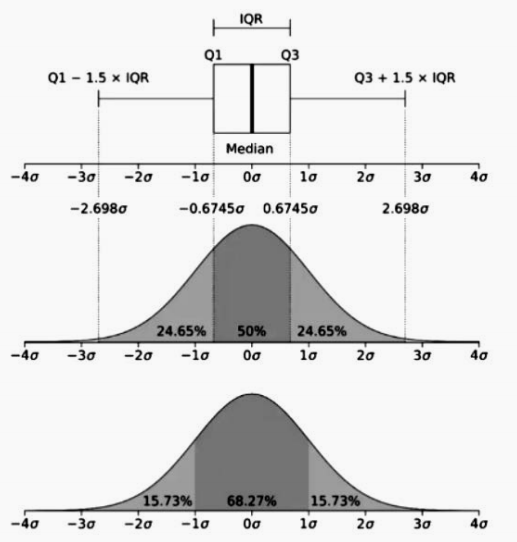
(2)在 Python 中計算百分位數:
NumPy 提供了一個非常方便的百分位數函數,可以計算分布中百分位數的值。我們已經使用 np.random.normal 函數創建了一個列表 vals,調用 np.percentile 函數就可以找出第
90 個百分位數的值,90%的數據都小于這個值。代碼如下:
import numpy as np
values=np.random.normal(0,0.5,10000)
x=np.percentile(values,90)
print(x) #0.6374509963913575
(3)矩:
矩就是用在概率密度函數中描述數據分布形狀的一個指標參數,它有一個非常棒的數學定義:
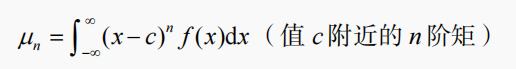
一階矩是均值,二階矩是方差,三階矩是偏度,四階矩是峰度。我們已經知道了什么是均值和方差。偏度表示數據的偏斜程度,即數據的尾部偏向哪一側。峰度表示數據分布有多尖銳,即從兩側向中間被擠壓的程度。
1)三階矩是偏度,要計算這個指標需要使用 SciPy包,而不是 NumPy。在很多科學計算包中,都有這個擴展包,比如 Enthought Canopy或 Anaconda。如果你導入了 SciPy,那么函數調用非常簡單。 vals 列表調用函數 sp.skew,就可以求出峰度值。因為這個值非常接近于 0,所以數據應該是 0 偏的。如果加入一些隨機變動,數據會變得略微左偏。實際上,在圖中的表現就是形狀有些抖動,就像是向負方向拉扯了一下。
import numpy as np
import scipy.stats as sp
values=np.random.normal(0,0.5,10000)
x=sp.skew(values)
print(x) #-0.009862010417180718
2)四階矩是峰度,描述了數據尾部的形狀。
峰度揭示了數據分布互相聯系的兩個特征:尾部的形狀以及頂部的尖銳程度。如果將分布的尾部壓得更扁,就會使得頂部更加尖銳。同樣,如果將分布的頂部壓下去一些,就會使尾部更加肥大,頂部更加平坦。這就是峰度的作用。
import numpy as np
import scipy.stats as sp
values=np.random.normal(0,0.5,10000)
x=sp.kurtosis(values) #峰度
print(x) #-0.00876087807733228
智能推薦
freemarker + ItextRender 根據模板生成PDF文件
1. 制作模板 2. 獲取模板,并將所獲取的數據加載生成html文件 2. 生成PDF文件 其中由兩個地方需要注意,都是關于獲取文件路徑的問題,由于項目部署的時候是打包成jar包形式,所以在開發過程中時直接安照傳統的獲取方法沒有一點文件,但是當打包后部署,總是出錯。于是參考網上文章,先將文件讀出來到項目的臨時目錄下,然后再按正常方式加載該臨時文件; 還有一個問題至今沒有解決,就是關于生成PDF文件...
電腦空間不夠了?教你一個小秒招快速清理 Docker 占用的磁盤空間!
Docker 很占用空間,每當我們運行容器、拉取鏡像、部署應用、構建自己的鏡像時,我們的磁盤空間會被大量占用。 如果你也被這個問題所困擾,咱們就一起看一下 Docker 是如何使用磁盤空間的,以及如何回收。 docker 占用的空間可以通過下面的命令查看: TYPE 列出了docker 使用磁盤的 4 種類型: Images:所有鏡像占用的空間,包括拉取下來的鏡像,和本地構建的。 Con...
requests實現全自動PPT模板
http://www.1ppt.com/moban/ 可以免費的下載PPT模板,當然如果要人工一個個下,還是挺麻煩的,我們可以利用requests輕松下載 訪問這個主頁,我們可以看到下面的樣式 點每一個PPT模板的圖片,我們可以進入到詳細的信息頁面,翻到下面,我們可以看到對應的下載地址 點擊這個下載的按鈕,我們便可以下載對應的PPT壓縮包 那我們就開始做吧 首先,查看網頁的源代碼,我們可以看到每一...
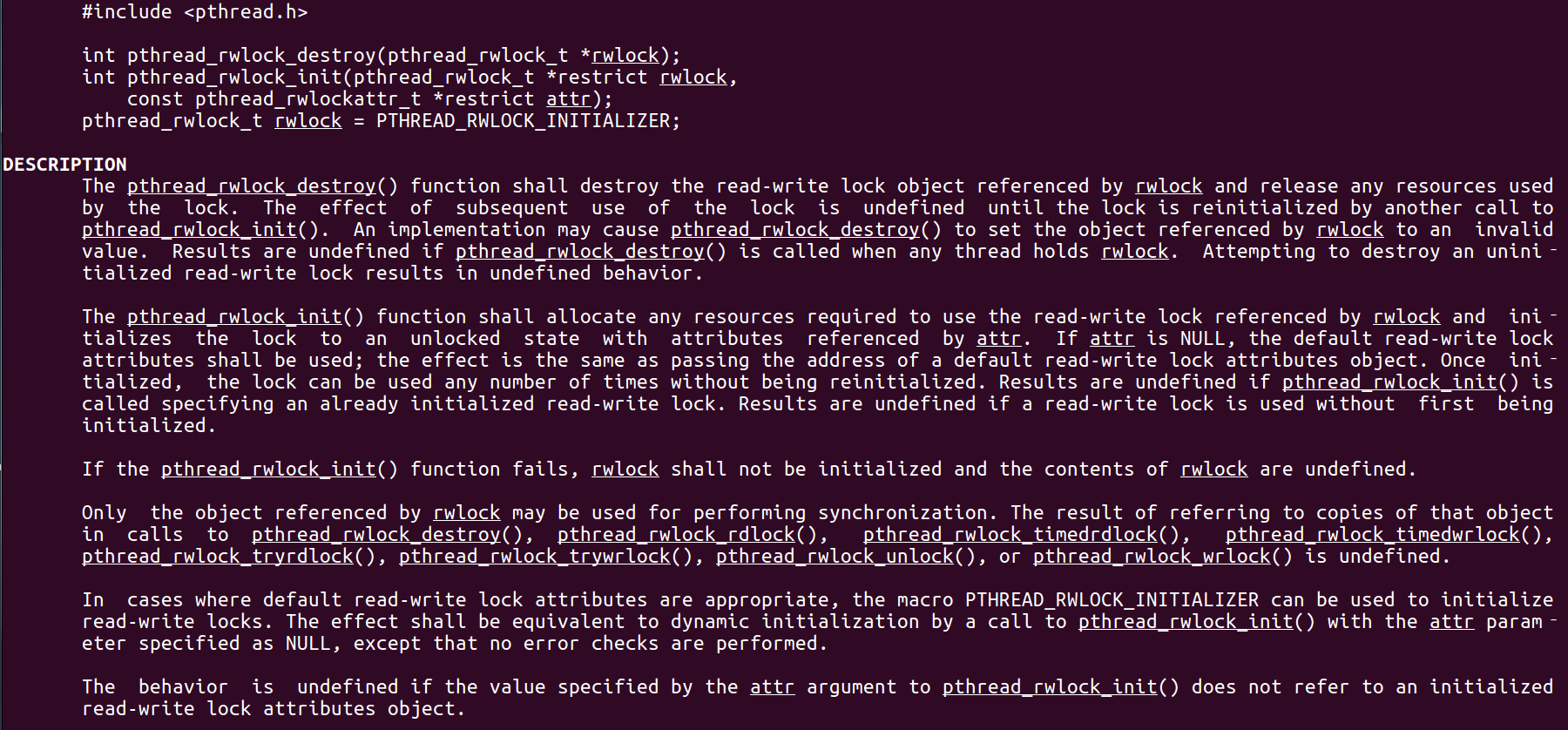
Linux C系統編程-線程互斥鎖(四)
互斥鎖 互斥鎖也是屬于線程之間處理同步互斥方式,有上鎖/解鎖兩種狀態。 互斥鎖函數接口 1)初始化互斥鎖 pthread_mutex_init() man 3 pthread_mutex_init (找不到的情況下首先 sudo apt-get install glibc-doc sudo apt-get install manpages-posix-dev) 動態初始化 int pthread_...
猜你喜歡
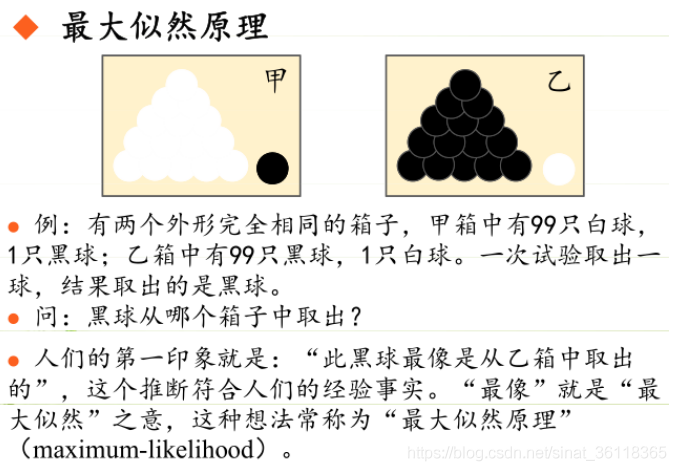
統計學習方法 - 樸素貝葉斯
引入問題:一機器在良好狀態生產合格產品幾率是 90%,在故障狀態生產合格產品幾率是 30%,機器良好的概率是 75%。若一日第一件產品是合格品,那么此日機器良好的概率是多少。 貝葉斯模型 生成模型與判別模型 判別模型,即要判斷這個東西到底是哪一類,也就是要求y,那就用給定的x去預測。 生成模型,是要生成一個模型,那就是誰根據什么生成了模型,誰就是類別y,根據的內容就是x 以上述例子,判斷一個生產出...
styled-components —— React 中的 CSS 最佳實踐
https://zhuanlan.zhihu.com/p/29344146 Styled-components 是目前 React 樣式方案中最受關注的一種,它既具備了 css-in-js 的模塊化與參數化優點,又完全使用CSS的書寫習慣,不會引起額外的學習成本。本文是 styled-components 作者之一 Max Stoiber 所寫,首先總結了前端組件化樣式中的最佳實踐原則,然后在此基...
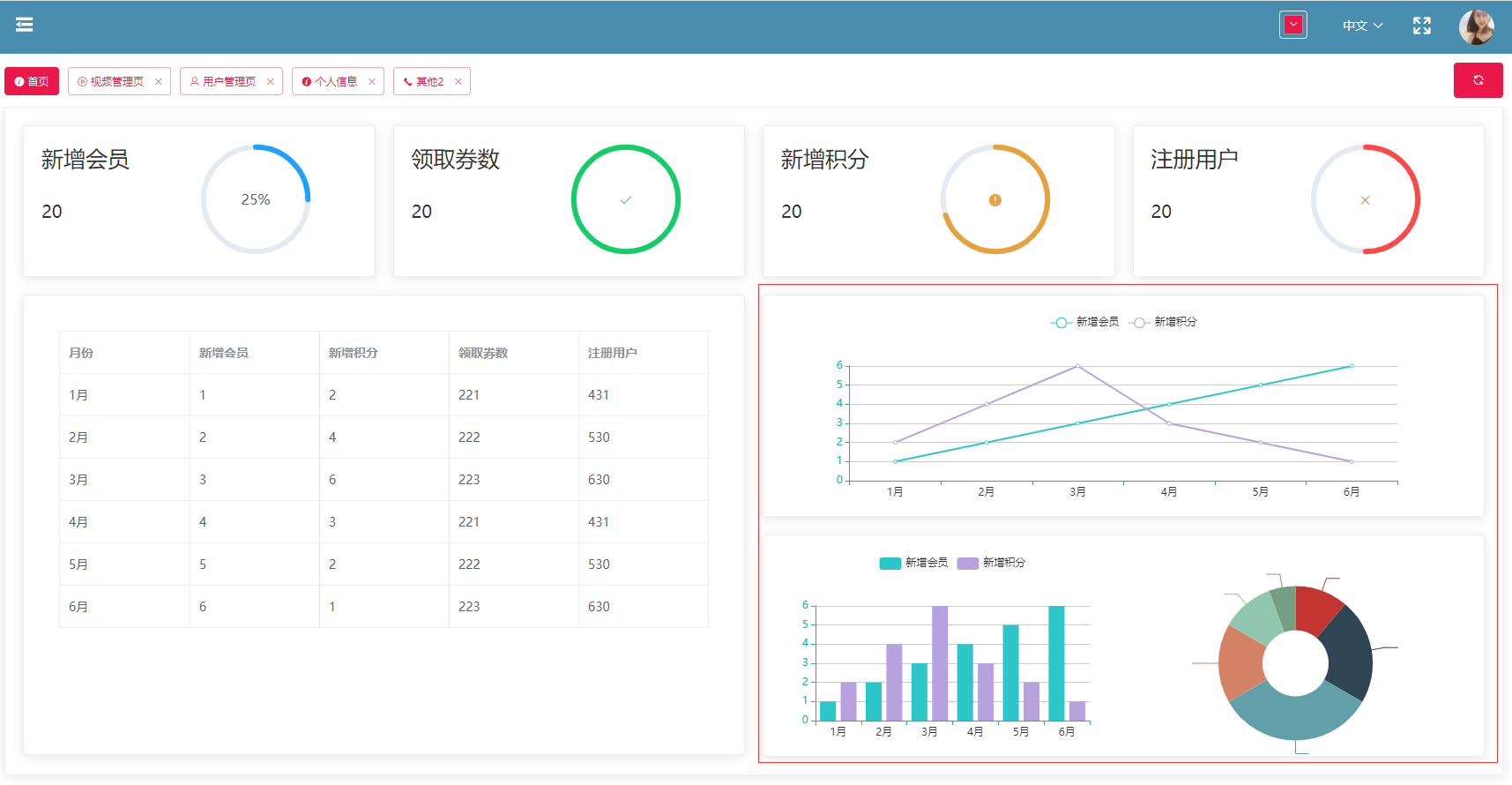
19.vue中封裝echarts組件
19.vue中封裝echarts組件 1.效果圖 2.echarts組件 3.使用組件 按照組件格式整理好數據格式 傳入組件 home.vue 4.接口返回數據格式...