穩態視覺誘發電位(SSVEP)識別| Extended Canonical Correlation Analysis, eCCA
標簽: 腦-機接口 算法【ML etc.】
Note: 在我有空的時候盡量把SSVEP流行的方法都開源出來,一是方便自己復習和鞏固,二是希望廣大網友能夠指出我思路中存在的一些問題。本人接觸這個領域時間較短,有什么紕漏請多指教。
前言
如果要說目前SSVEP識別中最流行的幾個方法,那么Extended Canonical Correlation Analysis(eCCA)1絕對是其中之一。目前來看,如果研究SSVEP算法,那么對比算法基本是TRCA或者eCCA2 3。此外,很多在線BCI系統也是采用該方法進行頻率識別。與TRCA這種具有自己數學模型的方法不同,eCCA僅是對CCA的一種計算結構調整。我們知道受試者的template中包含著一些潛在可利用的分類信息(相位等),eCCA在CCA基礎上考慮到了受試者template項。
算法
我們知道典型相關分析(CCA)是一種降維和評估兩組多維數據相關性的方法,它通過一對典型變量將兩組數據變為一維,使得兩者之間的相關系數最大。可以參考博客1、2。
CCA應用在SSVEP識別上得到了很好的效果,當已有受試者訓練數據的時候,我們能夠獲得三種多通道信號:測試數據,受試者訓練數據的平均以及構造的正余弦參考信號,其中,,分別表示通道數、采樣點數和測試集trial數。任意兩種信號可以根據CCA計算出空間濾波器。
按照排列組合方式來看,如果我們要根據其中兩個信號求空間濾波器,那么會有六種空間濾波器形式。六種空間濾波器會產生10個典型變量,然后每兩個典型變量之間又可以計算相關系數,那么就有45個相關系數。這個在Mohammad Hadi MehdizavarehI等人2020年發表在PLOS ONE上的文章4有詳述。但實際應用過程中,我們通常只取了三種空間濾波器形式(這里以Chen X等人PANS上的文章為例,第三項做了修正)分別為
- ,:測試數據和template之間;
- :測試數據和參考信號之間;
- :template和參考信號之間。
由上述空間濾波器,我們可以得到5個相關系數組合(這里的數量在不同的論文中不一致,最初提出eCCA的時候并沒有對為什么采用下述相關系數組合做解釋。),如下
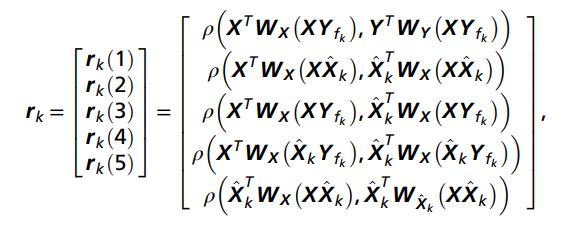
注:上述公式來自Chen X等人的論文,其中所對應的空間濾波器形式有誤,應該為。如果僅考慮第一項,那么算法變為標準的CCA;如果對相關系數進行融合,便可以得到k-th刺激下的相關系數。最后通過確認最大相關系數對應的刺激便可以實現分類
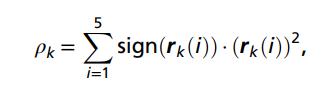
整個算法的計算結構為
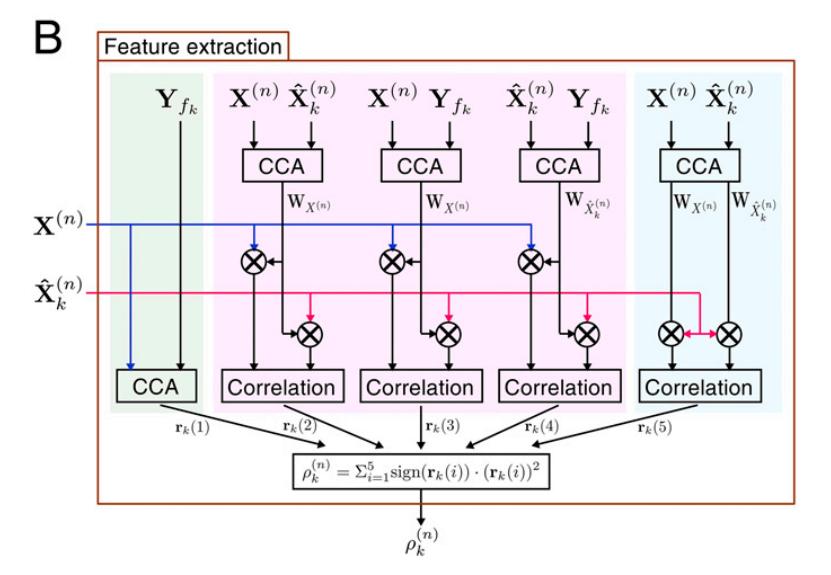
Matlab代碼
CCA
function [output1, output2] = CCA(signal1, signal2)
% Canonical Correlation Analysis, CCA
% Input:
% signal: #channels, #points
% Output:
% output1: spatial filter of signal1
% output2: spatial filter of signal2
%
X=signal1;
Y=signal2;
T=size(signal2, 2);
%compute covariance matrix
meanx=mean(X,2);
meany=mean(Y,2);
s11=0;s22=0;s12=0;s21=0;
for i1=1:T
s11=s11+(X(:,i1)-meanx)*(X(:,i1)-meanx)';
s22=s22+(Y(:,i1)-meany)*(Y(:,i1)-meany)';
s12=s12+(X(:,i1)-meanx)*(Y(:,i1)-meany)';
s21=s21+(Y(:,i1)-meany)*(X(:,i1)-meanx)';
end
s11=s11/(T-1);
s22=s22/(T-1);
s12=s12/(T-1);
s21=s21/(T-1);
%compute eigvalue and eigvector
[eigvectora,eigvaluea]=eig(inv(s11)*s12*inv(s22)*s21);
[eigvectorb,eigvalueb]=eig(inv(s22)*s21*inv(s11)*s12);
evaluea= diag(eigvaluea);
evalueb = diag(eigvalueb);
% correlation coefficient & canonical variates of signal1
[corrcoef1, index]= max(sqrt(evaluea));
output1 = eigvectora(:, index);
% correlation coefficient & canonical variates of signal2
[corrcoef2, index]= max(sqrt(evalueb));
output2 = eigvectorb(:, index);
end
對上述程序做簡要解釋
- 上述CCA求解采用的是特征值分解的方法,另外還可以參考SVD分解的做法;
- 通過CCA的推導過程可以看到,corrcoef1和corrcoef2相等,表示兩個輸入多通道信號的相關系數。在SSVEP中,標準CCA可采用該值直接輸出;
- 這個函數文件輸出的是兩個多通道信號的典型變量,即空間濾波器。
eCCA
% -------------------------------------------------------------------------
% Main for Extended Canonical Correlation Analysis[1]
%
% Dataset (Sx.mat):
% A 40-target SSVEP dataset recorded from a single subject. The stimuli
% were generated by the j oint frequency-phase modulation (JFPM)
% - Stimulus frequencies : 8.0 - 15.8 Hz with an interval of 0.2 Hz
% - Stimulus phases : 0pi, 0.5pi, 1.0pi, and 1.5pi
% - # of channels : Oz
% - # of recording blocks : 6
% - Data length of epochs : 1.5 [seconds]
% - Sampling rate : 250 [Hz]
% - Data format : # channels, # points, # targets, # blocks
%
% See also:
% CCA.m
%
% Reference:
% [1] Chen X, Wang Y, Nakanishi M, Gao X, Jung TP, Gao S (2015)
% High-speed spelling with a noninvasive brain-computer interface.
% PNAS 112:E6058-6067.
% -------------------------------------------------------------------------
clear all
close all
load ('Freq_Phase.mat')
load('subject1.mat')
eeg = subject1;
[N_channel, N_point, N_target, N_block] = size(eeg);
% sample rate
fs = 250;
t=1/fs:1/fs:N_point/fs;
%% ------------classification-------------
tic
% LOO cross-validation
for loocv_i = 1:N_block
Testdata = eeg(:, :, :, loocv_i);
Traindata = eeg;
Traindata(:, :, :, loocv_i) = [];
% number of harmonics
N_harmonic = 2;
for targ_i = 1:N_target
% Template
Template(:, :, targ_i) = mean(squeeze(Traindata(:,:,targ_i,:)),3);
% Reference
Y=[];
for har_i=1:N_harmonic
Y=cat(1,Y,cat(1, sin(2*pi*freqs(targ_i)*har_i*t), ...
cos(2*pi*freqs(targ_i)*har_i*t)));
end
Reference(:, :, targ_i) = Y;
end
% labels assignment according to testdata
truelabels=freqs;
N_testTrial=size(Testdata, 3);
for trial_i=1:N_testTrial
Allcoefficience = [];
for targ_j=1:length(freqs)
% ρ1 (Filter: Test data & Reference)
[wn1, wn2]= CCA(Testdata(:,:,trial_i), Reference(:, :, targ_j));
weighted_train = wn2'*Reference(:,:,targ_j);
weighted_test = wn1'*Testdata(:,:,trial_i);
coefficienceMatrix = corrcoef(weighted_test,weighted_train);
coefficience(1) = abs(coefficienceMatrix(1,2));
% ρ2 (Filter: Test data & Template)
[wn, ~] = CCA(Testdata(:,:,trial_i), Template(:, :, targ_j));
weighted_train = wn'*Template(:,:,targ_j);
weighted_test = wn'*Testdata(:,:,trial_i);
coefficienceMatrix = corrcoef(weighted_test,weighted_train);
coefficience(2) = coefficienceMatrix(1,2);
% ρ3 (Filter: Test data & Reference)
[wn, ~] = CCA(Testdata(:,:,trial_i), Reference(:, :, targ_j));
weighted_train = wn'*Template(:,:,targ_j);
weighted_test = wn'*Testdata(:,:,trial_i);
coefficienceMatrix = corrcoef(weighted_test,weighted_train);
coefficience(3) = coefficienceMatrix(1,2);
% ρ4 (Filter: Template & Reference)
[wn, ~] = CCA(Template(:, :, targ_j), Reference(:, :, targ_j));
weighted_train = wn'*Template(:,:,targ_j);
weighted_test = wn'*Testdata(:,:,trial_i);
coefficienceMatrix = corrcoef(weighted_test,weighted_train);
coefficience(4) = coefficienceMatrix(1,2);
% % ρ5 (Filter: Test data & Template)
% [wn1, wn2] = CCA(Testdata(:,:,trial_i), Template(:, :, targ_j));
% weighted_train = wn2'*Template(:,:,targ_j);
% weighted_test = wn1'*Template(:,:,targ_j);
% coefficienceMatrix = corrcoef(weighted_test,weighted_train);
% coefficience(5) = coefficienceMatrix(1,2);
% compute correlation values
Allcoefficience(targ_j) = sum(sign(coefficience).*coefficience.^2);
end % end targ_i
% target detection
[~, index] = max(Allcoefficience);
outputlabels(trial_i) = freqs(index);
end % end trial_i
trueNum = sum((outputlabels-truelabels)==0);
acc(loocv_i) = trueNum/length(truelabels);
fprintf('The %d-th CV accuracy is: %.4f, samples: %d/%d\n',loocv_i,...
acc(loocv_i),trueNum, N_testTrial)
end % end looCv_i
t=toc;
% data visualization
fprintf('\n-----------------------------------------\n')
disp(['total time: ',num2str(t),' s']);
fprintf('6-fold CV average accuracy is: %.4f\n',mean(acc))
對上述程序做簡要解釋
- 采用的數據為清華benchmark dataset 受試者1,數據已經經過濾波等預處理,數據長度為1.5s;
- 實驗中發現第五項的加入使得正確率降低,故只采用了四項的融合,和萬峰老師論文保持一致2 ;
- 完整代碼見我的倉庫。
前四項相關系數融合運行結果為
The 1-th CV accuracy is: 0.9250, samples: 37/40
The 2-th CV accuracy is: 0.9750, samples: 39/40
The 3-th CV accuracy is: 0.9750, samples: 39/40
The 4-th CV accuracy is: 0.9750, samples: 39/40
The 5-th CV accuracy is: 0.9750, samples: 39/40
The 6-th CV accuracy is: 0.9750, samples: 39/40
-----------------------------------------
total time: 175.7503 s
6-fold CV average accuracy is: 0.9667
五項相關系數融合運行結果為
The 1-th CV accuracy is: 0.5750, samples: 23/40
The 2-th CV accuracy is: 0.5750, samples: 23/40
The 3-th CV accuracy is: 0.7750, samples: 31/40
The 4-th CV accuracy is: 0.4750, samples: 19/40
The 5-th CV accuracy is: 0.6000, samples: 24/40
The 6-th CV accuracy is: 0.6500, samples: 26/40
-----------------------------------------
total time: 216.9206 s
6-fold CV average accuracy is: 0.6083
關于取哪些相關系數進行融合的問題,本文參考了四篇較新的文獻,其中采用5個相關系數融合是常用的選擇(都是清華的文章…)。但是在本文實驗后發現,第五項加入使正確率下降了…所以采用了萬峰老師的做法,只取了前四項,如果有問題希望各位能及時提出來。
References
- Chen X, Wang Y, Nakanishi M, Gao X, Jung TP, Gao S (2015) High-speed spelling with a noninvasive brain-computer interface. PNAS 112:E6058-6067.
- Wong CM, Wan F, Wang B, Wang Z, Nan W, Lao KF, Mak PU, Vai MI, Rosa A (2020) Learning across multi-stimulus enhances target recognition methods in SSVEP-based BCIs. Journal of neural engineering 17:016026.
- Xu M, Han J, Wang Y, Jung TP, Ming D (2020) Implementing over 100 command codes for a high-speed hybrid brain-computer interface using concurrent P300 and SSVEP features. IEEE Transactions on Biomedical Engineering.
- Mehdizavareh MH, Hemati S, Soltanian-Zadeh H (2020) Enhancing performance of subject-specific models via subject-independent information for SSVEP-based BCIs. PloS one 15:e0226048.
智能推薦
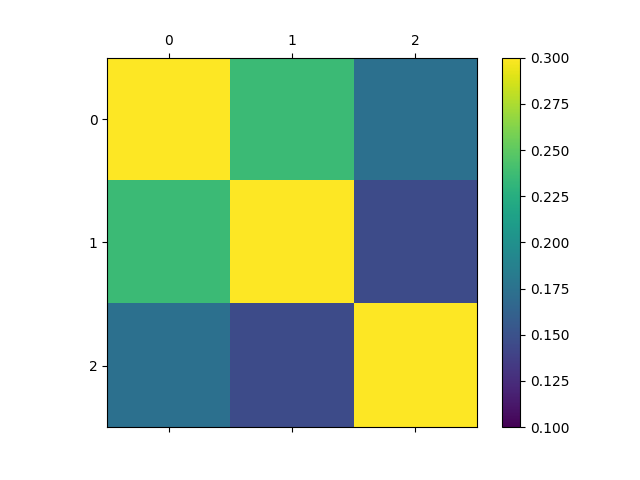
相關矩陣 Correlation matrix
根據提供的文件分析各個特征之間的相關性 Id MSSubClass MSZoning LotFrontage LotArea LandContour OverallCond YearBuilt YearRemodAdd RoofStyle MasVnrArea ExterQual ExterCond Heating HeatingQC CentralAir Electrical 1s...
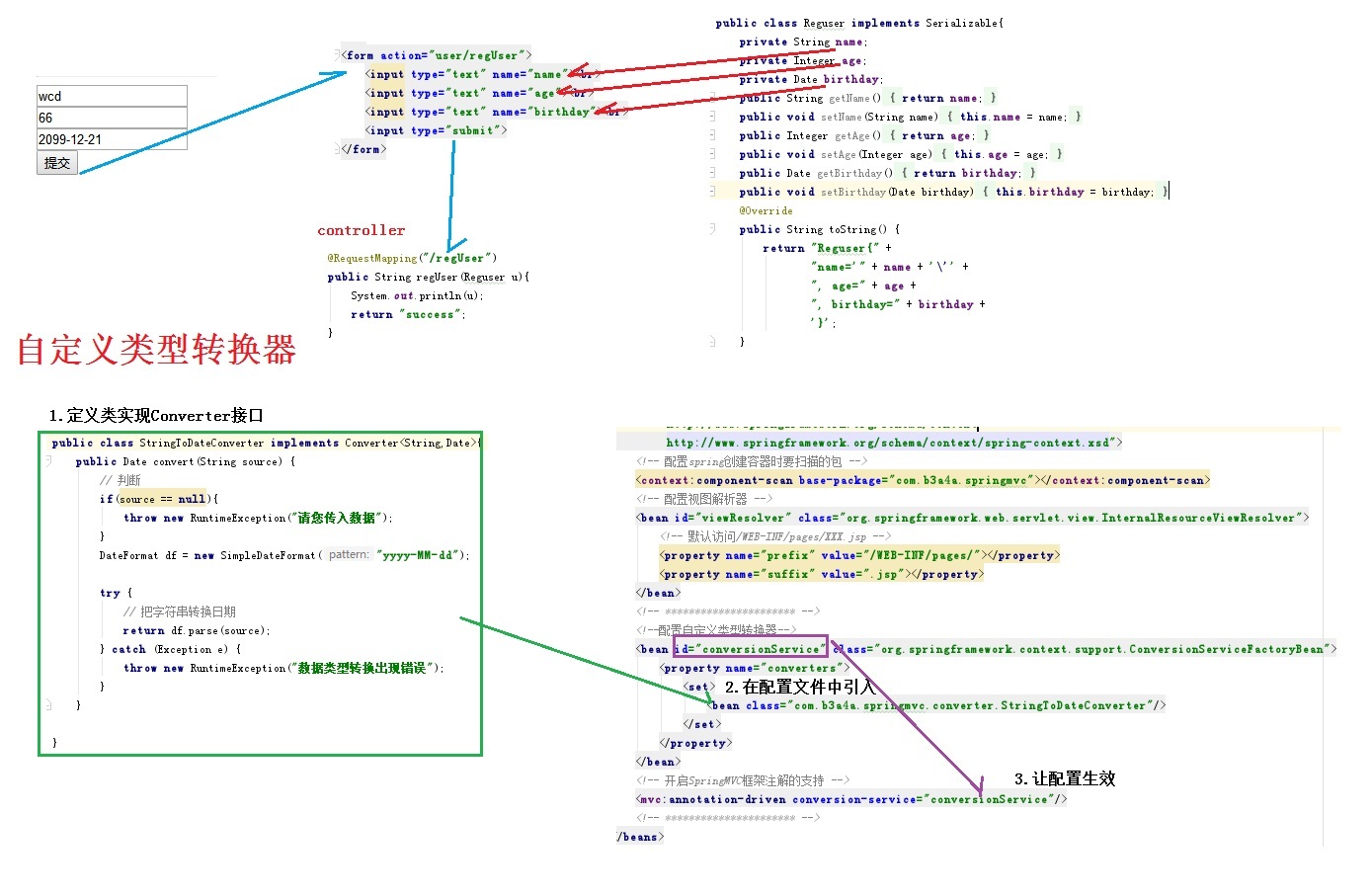
freemarker + ItextRender 根據模板生成PDF文件
1. 制作模板 2. 獲取模板,并將所獲取的數據加載生成html文件 2. 生成PDF文件 其中由兩個地方需要注意,都是關于獲取文件路徑的問題,由于項目部署的時候是打包成jar包形式,所以在開發過程中時直接安照傳統的獲取方法沒有一點文件,但是當打包后部署,總是出錯。于是參考網上文章,先將文件讀出來到項目的臨時目錄下,然后再按正常方式加載該臨時文件; 還有一個問題至今沒有解決,就是關于生成PDF文件...
電腦空間不夠了?教你一個小秒招快速清理 Docker 占用的磁盤空間!
Docker 很占用空間,每當我們運行容器、拉取鏡像、部署應用、構建自己的鏡像時,我們的磁盤空間會被大量占用。 如果你也被這個問題所困擾,咱們就一起看一下 Docker 是如何使用磁盤空間的,以及如何回收。 docker 占用的空間可以通過下面的命令查看: TYPE 列出了docker 使用磁盤的 4 種類型: Images:所有鏡像占用的空間,包括拉取下來的鏡像,和本地構建的。 Con...
猜你喜歡
requests實現全自動PPT模板
http://www.1ppt.com/moban/ 可以免費的下載PPT模板,當然如果要人工一個個下,還是挺麻煩的,我們可以利用requests輕松下載 訪問這個主頁,我們可以看到下面的樣式 點每一個PPT模板的圖片,我們可以進入到詳細的信息頁面,翻到下面,我們可以看到對應的下載地址 點擊這個下載的按鈕,我們便可以下載對應的PPT壓縮包 那我們就開始做吧 首先,查看網頁的源代碼,我們可以看到每一...
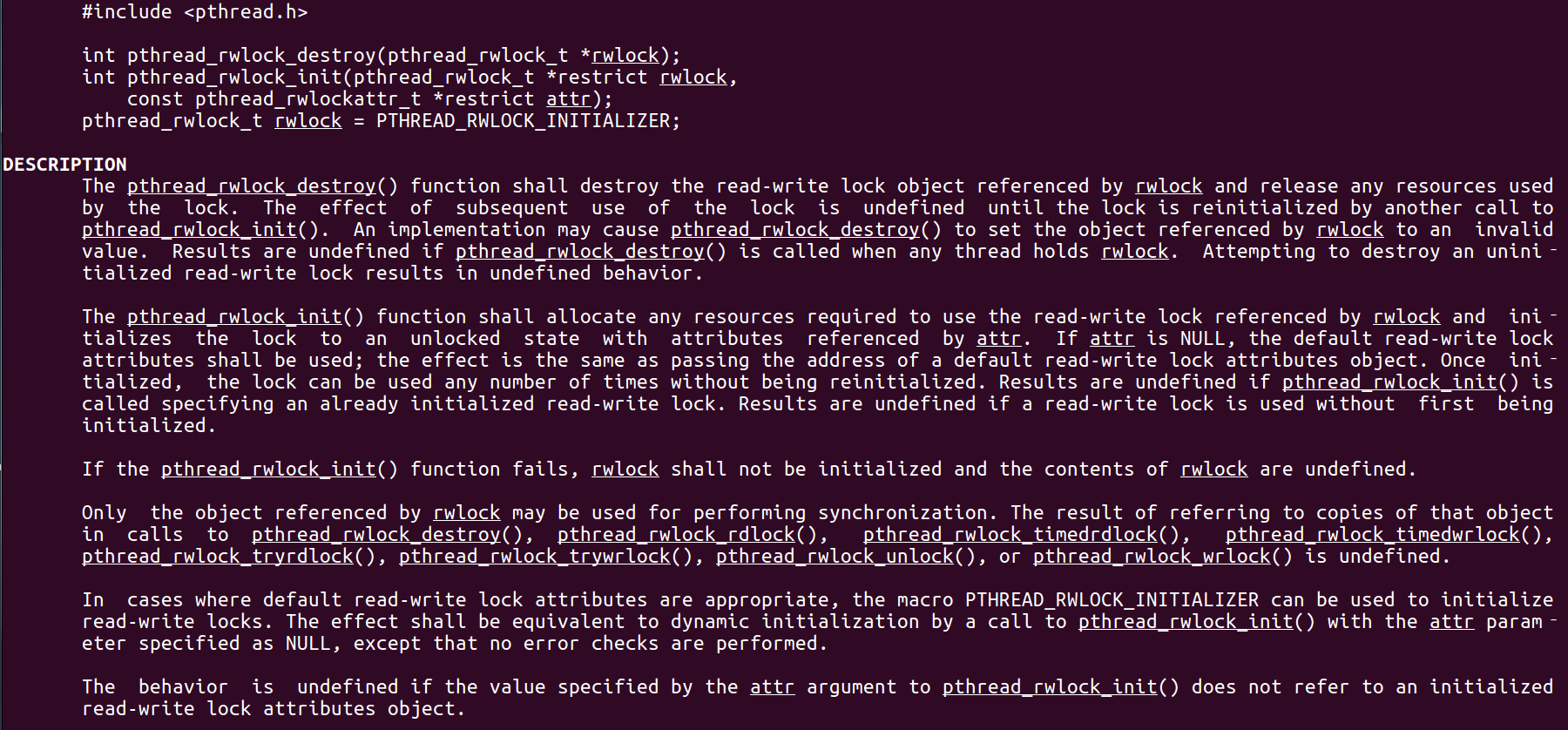
Linux C系統編程-線程互斥鎖(四)
互斥鎖 互斥鎖也是屬于線程之間處理同步互斥方式,有上鎖/解鎖兩種狀態。 互斥鎖函數接口 1)初始化互斥鎖 pthread_mutex_init() man 3 pthread_mutex_init (找不到的情況下首先 sudo apt-get install glibc-doc sudo apt-get install manpages-posix-dev) 動態初始化 int pthread_...
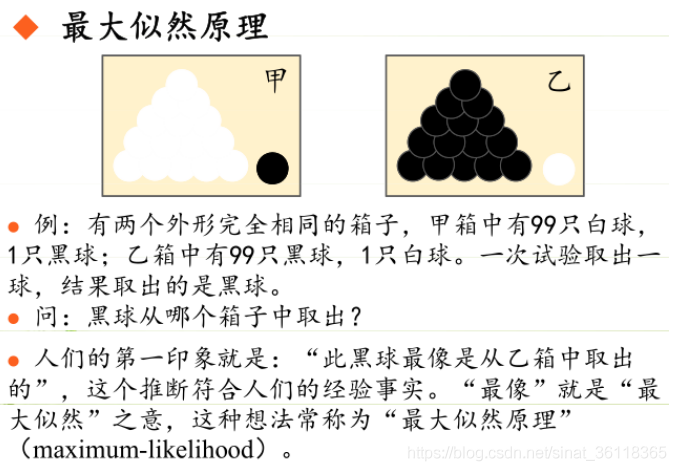
統計學習方法 - 樸素貝葉斯
引入問題:一機器在良好狀態生產合格產品幾率是 90%,在故障狀態生產合格產品幾率是 30%,機器良好的概率是 75%。若一日第一件產品是合格品,那么此日機器良好的概率是多少。 貝葉斯模型 生成模型與判別模型 判別模型,即要判斷這個東西到底是哪一類,也就是要求y,那就用給定的x去預測。 生成模型,是要生成一個模型,那就是誰根據什么生成了模型,誰就是類別y,根據的內容就是x 以上述例子,判斷一個生產出...
styled-components —— React 中的 CSS 最佳實踐
https://zhuanlan.zhihu.com/p/29344146 Styled-components 是目前 React 樣式方案中最受關注的一種,它既具備了 css-in-js 的模塊化與參數化優點,又完全使用CSS的書寫習慣,不會引起額外的學習成本。本文是 styled-components 作者之一 Max Stoiber 所寫,首先總結了前端組件化樣式中的最佳實踐原則,然后在此基...