import numpy as np
from lr_utils import load_dataset
#we only use these two modules currently
train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes = load_dataset()

m_train = train_set_x_orig.shape[0] #209 pic(train set)

m_test = test_set_x_orig.shape[0]   #50 pic(test set)
num_px = train_set_x_orig.shape[1]   #64 px

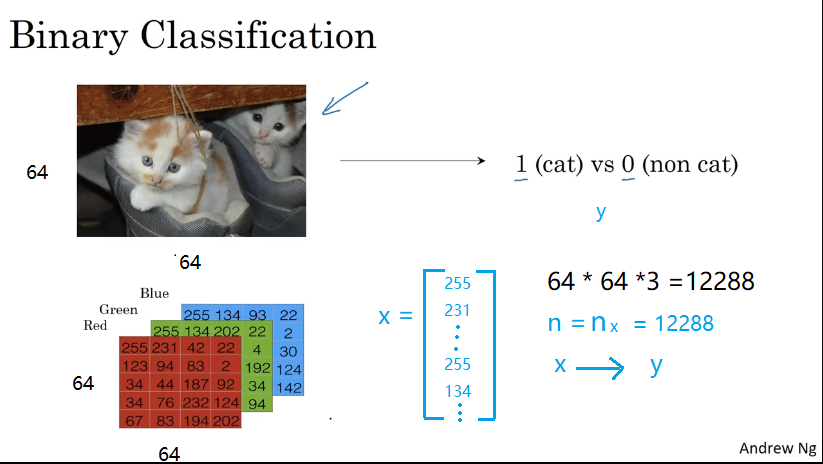
train_set_x_flatten = train_set_x_orig.reshape(m_train, num_px * num_px * 3).T     

test_set_x_flatten = test_set_x_orig.reshape(m_test, num_px * num_px * train_set_x_orig.shape[3]).T 

#209*64*64*3 train set /50*64*64*3 test set    12288*209         12288*50   

train_set_x = train_set_x_flatten / 255    #標準化操作 divide each pix by 255
test_set_x = test_set_x_flatten / 255

A、sigmoid(x)函數（upforward propagation ）

A=σ(wTX+b)=(a(0),a(1),...,a(m?1),a(m))

def sigmoid(x):

    s = 1.0 / (1 + 1 / np.exp(x))
    return s

B、initialize w&b

def initializewithzeros(dim):
    w = np.zeros((dim, 1))
    b = 0
    # we have to transfrom w in the following step, thus we initialize it as dim*1
    assert (w.shape == (dim, 1))
    assert (isinstance(b, float) or isinstance(b, int))

    return w, b

#     X equals to 12288*209 thus when we calculate the wTX+b, we have to do matrix transpose for w.(from 12288*1 to 1*12288)    w.T*X+b is 1*209

C、 propagate(forward, Cost calculation, backward gradient)

def propagate(w, b, X, Y):
    A = sigmoid(np.dot(w.T, X)+b)
    # shape of A: 1*209
    m = X.shape[1] #209
    cost = -(1.0 / m) * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))
#compared with train_set_y 

    dw = (1.0/m)* np.dot(X, (A - Y).T)
    # shape of dw: [64*64*3 1]
    db = 1.0 / m * np.sum(A - Y, axis=1, keepdims=True)
    cost = np.squeeze(cost)
    assert (cost.shape == ())
    assert (dw.shape == w.shape)
    assert (db.dtype == float)

    grads = {"dw": dw,
             "db": db
             }

    return grads, cost

calculate cost function：

    
                                            J=?1m∑mi=1y(i)log(a(i))+(1?y(i))log(1?a(i))

calculate backward gradient:         

D,  using dw,db to update w&b

def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost=True):
    costs = []



    for i in range(num_iterations):
        grads, cost = propagate(w, b, X, Y)

        dw = grads["dw"]
        db = grads["db"]
        if i % 100 == 0:
            costs.append(cost)
        w = w - dw * learning_rate
        b = b - db * learning_rate

        if print_cost and i % 100 == 0:
            print("Cost after iteration %i:%f" % (i, cost))

        params = {"w": w,
                  "b": b}
        grads = {"dw": dw,
                 "db": db
                 }

    return params, grads, costs

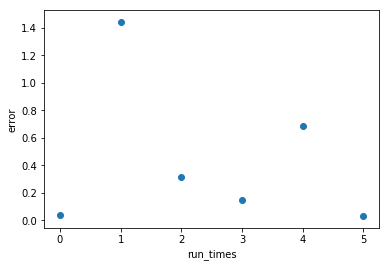
w and b update step by step thus the w and b will be more accurate, the output will be coincided with the model(iteration time)

E,  Prediction (get the output y_prediction)

def predict(w, b, X):
    m = X.shape[1]
    y_prediction = np.zeros((1, m))
#    w = w.reshape(X.shape[0], 1)
    A = sigmoid(np.dot(w.T, X) + b)
    for i in range(A.shape[1]):
        y_prediction = np.floor(A + 0.5)

    assert (y_prediction.shape == (1, m))

    return y_prediction

m equals to 209,  then we set an blank matrix(y_prediction) to save the data.

w equals to 12288*1 not necessary here!

A equals to 1*209, it proves the output of(y/n) every pic.

F , merge into the model function

def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
    w, b = initializewithzeros(X_train.shape[0])
    parameters, gradients, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)

    w = parameters['w']
    b = parameters['b']

    Y_prediction_train = predict(w, b, X_train)
    Y_prediction_test = predict(w, b, X_test)

    print("train accuracy:{} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))

    print("test accuracy:{} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))

    d = {"costs": costs,
         "Y_prediction_test": Y_prediction_test,
         "Y_prediction_train": Y_prediction_train,
         "w": w,
         "b": b,
         "learning_rate": learning_rate,
         "num_iterations": num_iterations}

    return d

get the prediction by using the predict function 

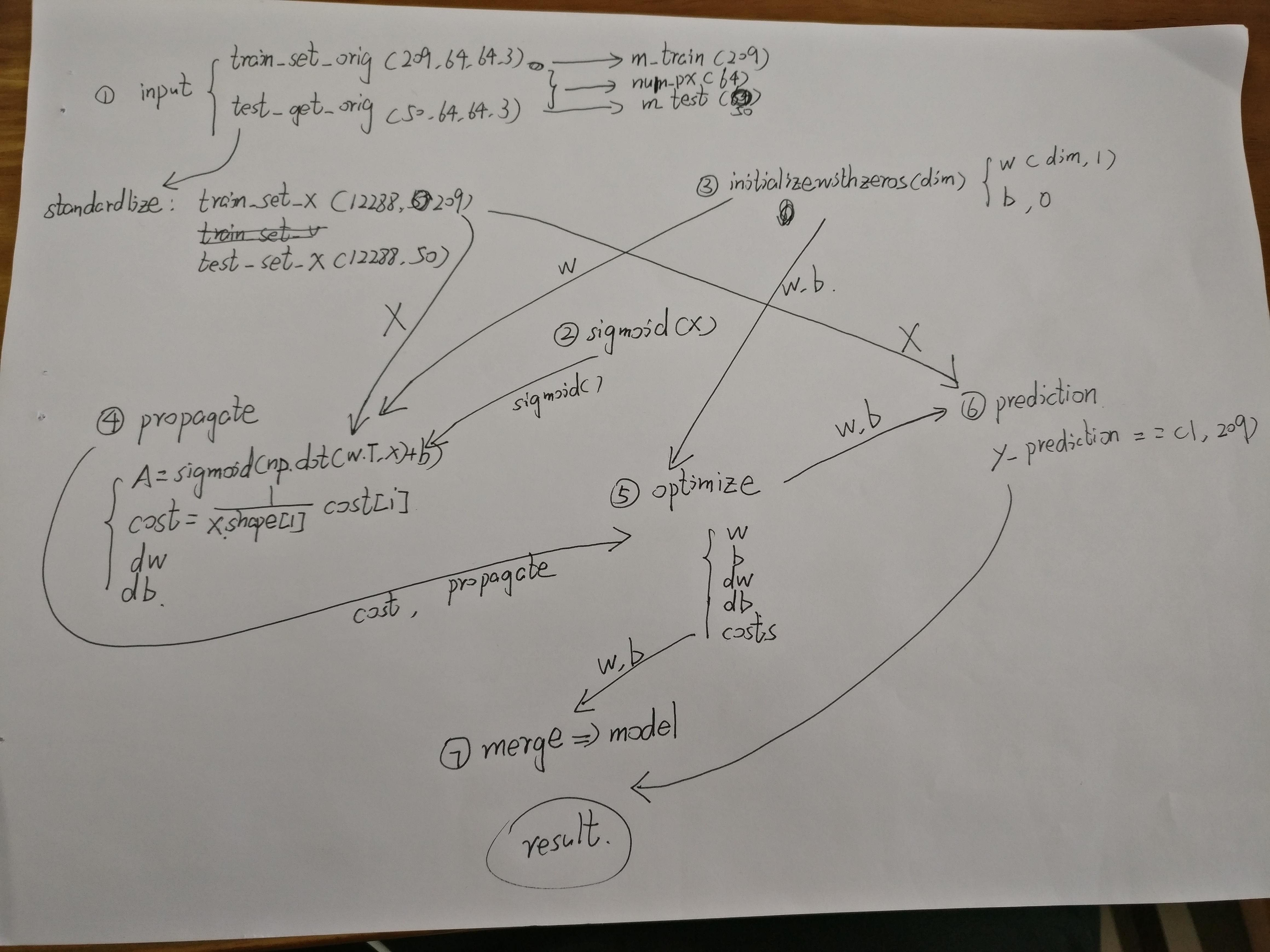
later on , I will also attach the mindnode pic for chapter 1 and 2, which is very useful for us to illustrate the total flow.