• <noscript id="e0iig"><kbd id="e0iig"></kbd></noscript>
  • <td id="e0iig"></td>
  • <option id="e0iig"></option>
  • <noscript id="e0iig"><source id="e0iig"></source></noscript>

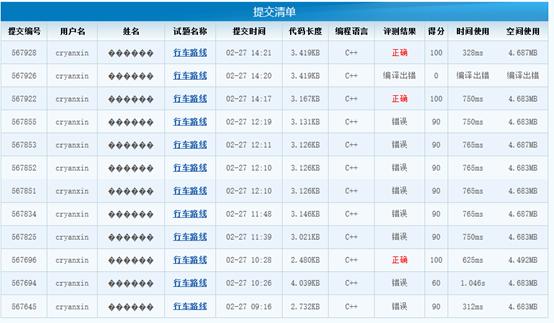
  • CCF 2017年12月第4題-行車路線

    標簽： CCF

    2017年12月第4題-行車路線

    這一題是最短路問題，稍微有些變形，因為需要處理大路和小路這兩種情況，其中小路的增長并不是線性的，所以需要對小路進行一遍預處理。思路是使用弗洛伊德算法和迪杰斯特拉結合。用弗洛伊德算法處理小路，用迪杰斯特拉算法處理總的距離。但不得不說這一題的測試數據十分的弱，即使是只使用迪杰斯特拉算法也可以過100%的測試用例。先貼一個第一遍的錯誤代碼。

    #include<iostream>
#include<vector>
#include<set>
using namespace std;
#define MAX 1000005
int main()
{
    int n;
    long long m;
    cin >> n; cin >> m;
    long long * Big[505];//用于存儲由某個端點發出的大路
    long long * Small[505];//用于存儲由某個端點發出的小路
    long long Sdist[505];//用于計算前驅為小路的當前最小距離
    long long Bdist[505];//用于計算前驅為大路的當前最小距離
    long long LSdist[505];//用于計算累積小路距離
    for (int i = 0; i <= n; ++i)
    {
        long long *A = new long long[505];
        long long *B = new long long[505];
        for (int j = 0; j < 505;++j)
        {
            A[j] = MAX;
            B[j] = MAX;
        }
        Big[i] = A;
        Small[i] = B;
    }
    for (long long i = 0; i < m; ++i)
    {
        int t, a, b;
        long long c;
        cin >> t; cin >> a; cin >> b; cin >> c;
        if (t == 0 &&Big[b][a]>c)
        {

            Big[b][a] = c;
            Big[a][b] = c;
;
        }
        else if(t==1 &&Small[b][a]>c)
        {
            Small[b][a] = c;
            Small[a][b] = c;
        }
    }
    /*初始化最短路徑*/
    for (int i = 0; i <= n; ++i)
    {
        Sdist[i] = MAX;
        Bdist[i] = MAX;
        LSdist[i] = 0;
    }
    Sdist[1] = 0;
    Bdist[1] = 0;
    int pre = 1;//用于記錄上一個加入進來的點的編號
    int ptype = 0;//用于記錄上一個加入進來的路的類型
    set<int> Brst;
    set<int> Srst;
    Brst.insert(1);
    Srst.insert(1);
    for (int i = 0; i <= 2*n; ++i)
    {
        if (ptype == 0)
        {
            /*如果前驅結點路是大路*/
            for (int j = 1; j <= n; ++j)
            {
                /*更新距離*/
                if (Small[pre][j]!=MAX&&Bdist[pre] + Small[pre][j]* Small[pre][j] < Sdist[j])
                {
                    Sdist[j] = Bdist[pre] + Small[pre][j] * Small[pre][j];
                    LSdist[j] = Small[pre][j];
                }
                if (Big[pre][j]!=MAX&&Bdist[pre] + Big[pre][j] < Bdist[j])
                {
                    Bdist[j] = Bdist[pre] + Big[pre][j];
                }
            }

        }
        if (ptype == 1)
        {
            /*如果前驅結點是小路*/
            for (int j = 1; j <= n;++j)
            {
                if (Small[pre][j]!=MAX&&Sdist[pre] + Small[pre][j] * Small[pre][j] + 2 * Small[pre][j] *LSdist[pre] < Sdist[j])
                {
                    Sdist[j] = Sdist[pre] + Small[pre][j] *Small[pre][j] + 2 * Small[pre][j] *LSdist[pre];
                    LSdist[j] = LSdist[pre] + Small[pre][j];
                }
                if (Big[pre][j]!=MAX&&Sdist[pre] + Big[pre][j] < Bdist[j])
                {
                    Bdist[j] = Sdist[pre] + Big[pre][j];
                }
            }
        }
        int min=MAX;
        for (int j = 1; j <= n; ++j)
        {
            if (Sdist[j] < min&&Srst.find(j) == Srst.end())
            {
                min = Sdist[j];
                ptype = 1;
                pre = j;
            }
            if (Bdist[j] < min&&Brst.find(j) == Brst.end())
            {
                min = Bdist[j];
                ptype = 0;
                pre = j;
            }
        }
        if (ptype == 1)Srst.insert(pre);
        else Brst.insert(pre);
        if (pre == n)break;

    }
    if (Bdist[n] < Sdist[n])cout << Bdist[n];
    else cout << Sdist[n];
    system("pause");
    return 0;
}

    代碼很簡單，就是對迪杰斯特拉算法進行了一下變形。 考慮前驅是大路或者前驅是小路這兩種情況，最后拿到了100分分。

     

    雖然第一遍代碼能拿到100分但是明顯有一個問題就是在前驅是小路時，并不是總路長最短就是最優的，還需要考慮已經累計的小路的長度。所以這題的測試用例，十分的不走心。

    對于這種問題其實可以先抽取出所有的小路邊，然后用弗洛伊德算法計算出多源最短路，最后將所有的多源最短路加入到小路邊，然后使用上面的思路就沒問題了。改進后的代碼

    Tips:

    這一題有兩個測試用例會有重邊（唉。。。）。

    // 20171203-行車路線.cpp: 定義控制臺應用程序的入口點。
//

#include "stdafx.h"
#include<iostream>
#include<vector>
#include<set>
using namespace std;
#define MAX 10000005
int main()
{
	int n;
	long long m;
	cin >> n; cin >> m;
	long long * Big[505];//用于存儲由某個端點發出的大路
	long long * Small[505];//用于存儲由某個端點發出的小路
	long long Sdist[505];//用于計算前驅為小路的當前最小距離
	long long Bdist[505];//用于計算前驅為大路的當前最小距離
	long long LSdist[505];//用于計算累積小路距離
	for (int i = 0; i <= n; ++i)
	{
		long long *A = new long long[505];
		long long *B = new long long[505];
		for (int j = 0; j < 505; ++j)
		{
			A[j] = MAX;
			B[j] = MAX;
		}
		Big[i] = A;
		Small[i] = B;
	}
	for (long long i = 0; i < m; ++i)
	{
		int t, a, b;
		long long c;
		cin >> t; cin >> a; cin >> b; cin >> c;
		if (t == 0&&Big[b][a]>c)
		{

			Big[b][a] = c;
			Big[a][b] = c;
		}
		else if(t==1&&Small[b][a]>c)
		{
			Small[b][a] = c;
			Small[a][b] = c;
		}
	}
	/*利用弗洛伊德算法加入一些邊*/
	for (int i = 1; i <= n; ++i)
	{
		for (int j = 1; j <= n; ++j)
		{
			for (int k = 1; k <= n; ++k)
			{
				if (Small[i][k] > Small[i][j] + Small[j][k])
				{
					Small[i][k] = Small[i][j] + Small[j][k];
				}
			}
		}
	}
	/*初始化最短路徑*/
	for (int i = 0; i <= n; ++i)
	{
		Sdist[i] = MAX;
		Bdist[i] = MAX;
		LSdist[i] = 0;
	}
	Sdist[1] = 0;
	Bdist[1] = 0;
	int pre = 1;//用于記錄上一個加入進來的點的編號
	int ptype = 0;//用于記錄上一個加入進來的路的類型
	set<int> Brst;
	set<int> Srst;
	Brst.insert(1);
	Srst.insert(1);
	for (int i = 0; i <= 2 * n; ++i)
	{
		if (ptype == 0)
		{
			/*如果前驅結點路是大路*/
			for (int j = 1; j <= n; ++j)
			{
				/*更新距離*/
				if (Small[pre][j] != MAX && Bdist[pre] + Small[pre][j] * Small[pre][j] < Sdist[j])
				{
					Sdist[j] = Bdist[pre] + Small[pre][j] * Small[pre][j];
					LSdist[j] = Small[pre][j];
				}
				if (Big[pre][j] != MAX && Bdist[pre] + Big[pre][j] < Bdist[j])
				{
					Bdist[j] = Bdist[pre] + Big[pre][j];
				}
			}

		}
		if (ptype == 1)
		{
			/*如果前驅結點是小路*/
			for (int j = 1; j <= n; ++j)
			{
				/*這里注意當前驅結點是小路時不能再走小路（因為已經進行了弗洛伊德預處理）*/
				/*
				if (Small[pre][j] != MAX && Sdist[pre] + Small[pre][j] * Small[pre][j] + 2 * Small[pre][j] * LSdist[pre] < Sdist[j])
				{
					Sdist[j] = Sdist[pre] + Small[pre][j] * Small[pre][j] + 2 * Small[pre][j] * LSdist[pre];
					LSdist[j] = LSdist[pre] + Small[pre][j];
				}
				*/
				if (Big[pre][j] != MAX && Sdist[pre] + Big[pre][j] < Bdist[j])
				{
					Bdist[j] = Sdist[pre] + Big[pre][j];
				}
			}
		}
		long long min = MAX;
		for (int j = 1; j <= n; ++j)
		{
			if (Bdist[j] <= min&&Brst.find(j) == Brst.end())
			{
				min = Bdist[j];
				ptype = 0;
				pre = j;
			}
			if (Sdist[j] < min&&Srst.find(j) == Srst.end())
			{
				min = Sdist[j];
				ptype = 1;
				pre = j;
			}
			
		}
		if (ptype == 1)Srst.insert(pre);
		else Brst.insert(pre);
		if (pre == n)break;

	}
	if (Bdist[n] < Sdist[n])cout << Bdist[n];
	else cout << Sdist[n];
	system("pause");
	return 0;
}

    版權聲明：本文為cryanxin原創文章，遵循 CC 4.0 BY-SA 版權協議，轉載請附上原文出處鏈接和本聲明。
    本文鏈接：https://blog.csdn.net/cryanxin/article/details/79447928

    智能推薦

    CCF2018年3月第2題（碰撞的小球）Java解法

    題目描述：數軸上有長度為L（L為偶數）的線段，左端點0，右端點L。n個小球開始都是向右，且都在偶數坐標上，速度大小為1單位長度每秒。 當小球到達端點（0或L）時，立即反向，速度不變；當兩個小球相撞（在同一位置），立即反向，速度不變。 現在告訴你線段長度L，小球數量n，以及n個小球初始位置，請計算t秒之后各個小球的位置。 提示：同一時刻同一位置最多只有兩個小球相撞，由于速度始終不變，所以碰撞時間也是...

    CCF CSP 2016年9月第3題 爐石傳說（模擬）

    問題描述 試題編號： 201609-3 試題名稱： 爐石傳說 時間限制： 1.0s 內存限制： 256.0MB 問題描述： 問題描述 　　《爐石傳說：魔獸英雄傳》（Hearthstone: Heroes of Warcraft，簡稱爐石傳說）是暴雪娛樂開發的一款集換式卡牌游戲（如下圖所示）。游戲在一個戰斗棋盤上進行，由兩名玩家輪流進行操作，本題所使用的爐石傳說游戲的簡化規則如下： 　　* 玩家會控...

    HTML中常用操作關于：頁面跳轉，空格

    1.頁面跳轉 2.空格的代替符...

    freemarker + ItextRender 根據模板生成PDF文件

    1. 制作模板 2. 獲取模板，并將所獲取的數據加載生成html文件 2. 生成PDF文件 其中由兩個地方需要注意，都是關于獲取文件路徑的問題，由于項目部署的時候是打包成jar包形式，所以在開發過程中時直接安照傳統的獲取方法沒有一點文件，但是當打包后部署，總是出錯。于是參考網上文章，先將文件讀出來到項目的臨時目錄下，然后再按正常方式加載該臨時文件； 還有一個問題至今沒有解決，就是關于生成PDF文件...

    電腦空間不夠了？教你一個小秒招快速清理 Docker 占用的磁盤空間！

    Docker 很占用空間，每當我們運行容器、拉取鏡像、部署應用、構建自己的鏡像時，我們的磁盤空間會被大量占用。 如果你也被這個問題所困擾，咱們就一起看一下 Docker 是如何使用磁盤空間的，以及如何回收。 docker 占用的空間可以通過下面的命令查看： TYPE 列出了docker 使用磁盤的 4 種類型： Images：所有鏡像占用的空間，包括拉取下來的鏡像，和本地構建的。 Con...

    猜你喜歡

    requests實現全自動PPT模板

    http://www.1ppt.com/moban/ 可以免費的下載PPT模板，當然如果要人工一個個下，還是挺麻煩的，我們可以利用requests輕松下載 訪問這個主頁，我們可以看到下面的樣式 點每一個PPT模板的圖片，我們可以進入到詳細的信息頁面，翻到下面，我們可以看到對應的下載地址 點擊這個下載的按鈕，我們便可以下載對應的PPT壓縮包 那我們就開始做吧 首先，查看網頁的源代碼，我們可以看到每一...

    SpringMvc自定義類型轉換器步驟

    ...

    Linux C系統編程-線程互斥鎖（四）

    互斥鎖 互斥鎖也是屬于線程之間處理同步互斥方式，有上鎖/解鎖兩種狀態。 互斥鎖函數接口 1）初始化互斥鎖 pthread_mutex_init() man 3 pthread_mutex_init (找不到的情況下首先 sudo apt-get install glibc-doc sudo apt-get install manpages-posix-dev) 動態初始化 int pthread_...

    統計學習方法 - 樸素貝葉斯

    引入問題：一機器在良好狀態生產合格產品幾率是 90%，在故障狀態生產合格產品幾率是 30%，機器良好的概率是 75%。若一日第一件產品是合格品，那么此日機器良好的概率是多少。 貝葉斯模型 生成模型與判別模型 判別模型，即要判斷這個東西到底是哪一類，也就是要求y，那就用給定的x去預測。 生成模型，是要生成一個模型，那就是誰根據什么生成了模型，誰就是類別y，根據的內容就是x 以上述例子，判斷一個生產出...

    styled-components —— React 中的 CSS 最佳實踐

    https://zhuanlan.zhihu.com/p/29344146 Styled-components 是目前 React 樣式方案中最受關注的一種，它既具備了 css-in-js 的模塊化與參數化優點，又完全使用CSS的書寫習慣，不會引起額外的學習成本。本文是 styled-components 作者之一 Max Stoiber 所寫，首先總結了前端組件化樣式中的最佳實踐原則，然后在此基...

    精品国产乱码久久久久久蜜桃不卡