【藍橋杯】01背包問題

一、問題描述

有 N 個物品，并且每個物品都有一個重量 W 和一個價值 V。你有一個能裝 M 重量的背包，問怎么裝才能使所裝的價值最大(每個物品只有一個)

輸入：

輸入的第一行包含兩個整數 n, m，分別表示物品的個數和背包能裝的重量

以后N行每行兩個數 Wi 和 Vi,表示物品的重量和價值

輸出：

輸出1行，包含一個整數，表示最大價值。

樣例輸入：
3 5
2 3
3 5
4 7
樣例輸出：
8

二、解題思路

解題方法：動態規劃

記 f(i, W)：當背包容量為 W 時，現有 i 件物品可以裝，所能裝入背包的最大值(即：f(3, 5))
那么現在分為兩種情況：

a. 不裝入第 i 件物品，f(i-1, W)

b. 裝入第 i 件物品，f(i-1, W - w[i]) + v[i]

由此可以推出狀態轉移方程：
f ( i , W ) = { f ( i ? 1 , W ) w[i]>W(物品太重) m a x { f ( i ? 1 , W ) , f ( i ? 1 , W ? w [ i ] ) + v [ i ] } w[i]<=W f(i,W) = \begin{cases} f(i-1,W) & \text{w[i]>W(物品太重)} \\ max\{f(i-1,W),& f(i-1,W-w[i])+v[i]\}& \text{w[i]<=W} \end{cases} f(i,W)={f(i?1,W)max{f(i?1,W),?w[i]>W(物品太重)f(i?1,W?w[i])+v[i]}?w[i]<=W?
即：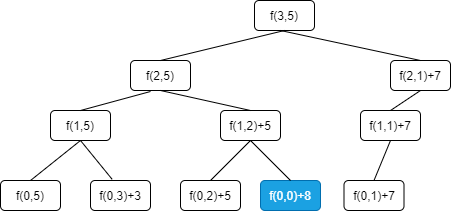

通過填寫表把所有已經解決的子問題答案紀錄下來，在新問題里需要用到的子問題可以直接提取，避免了重復計算，從而節約了時間，所以在問題滿足最優性原理之后，用動態規劃解決問題的核心就在于填表，表填寫完畢，最優解也就找到

三、AC代碼如下

#include<bits/stdc++.h>
using namespace std;
int dp[201][5001];
int main()
{
    int n,m,z;
    cin>>n>>m;
    vector<int> w,v;
    for(int i=1;i<=n;i++){
        cin>>z;
        w.push_back(z);
        cin>>z;
        v.push_back(z);
    }
    //規劃最優解
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(j<w[i-1]){
                dp[i][j] = dp[i-1][j];
                continue;
            }
            dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i-1]]+v[i-1]);
        }
    }
    cout<<dp[n][m]<<endl;
    return 0;
}

本文鏈接：https://blog.csdn.net/xwmrqqq/article/details/109210578

智能推薦

電腦空間不夠了？教你一個小秒招快速清理 Docker 占用的磁盤空間！

Docker 很占用空間，每當我們運行容器、拉取鏡像、部署應用、構建自己的鏡像時，我們的磁盤空間會被大量占用。如果你也被這個問題所困擾，咱們就一起看一下 Docker 是如何使用磁盤空間的，以及如何回收。 docker 占用的空間可以通過下面的命令查看： TYPE 列出了docker 使用磁盤的 4 種類型： Images：所有鏡像占用的空間，包括拉取下來的鏡像，和本地構建的。 Con...

requests實現全自動PPT模板

http://www.1ppt.com/moban/ 可以免費的下載PPT模板，當然如果要人工一個個下，還是挺麻煩的，我們可以利用requests輕松下載訪問這個主頁，我們可以看到下面的樣式點每一個PPT模板的圖片，我們可以進入到詳細的信息頁面，翻到下面，我們可以看到對應的下載地址點擊這個下載的按鈕，我們便可以下載對應的PPT壓縮包那我們就開始做吧首先，查看網頁的源代碼，我們可以看到每一...

互斥鎖互斥鎖也是屬于線程之間處理同步互斥方式，有上鎖/解鎖兩種狀態。互斥鎖函數接口 1）初始化互斥鎖 pthread_mutex_init() man 3 pthread_mutex_init (找不到的情況下首先 sudo apt-get install glibc-doc sudo apt-get install manpages-posix-dev) 動態初始化 int pthread_...

統計學習方法 - 樸素貝葉斯

引入問題：一機器在良好狀態生產合格產品幾率是 90%，在故障狀態生產合格產品幾率是 30%，機器良好的概率是 75%。若一日第一件產品是合格品，那么此日機器良好的概率是多少。貝葉斯模型生成模型與判別模型判別模型，即要判斷這個東西到底是哪一類，也就是要求y，那就用給定的x去預測。生成模型，是要生成一個模型，那就是誰根據什么生成了模型，誰就是類別y，根據的內容就是x 以上述例子，判斷一個生產出...