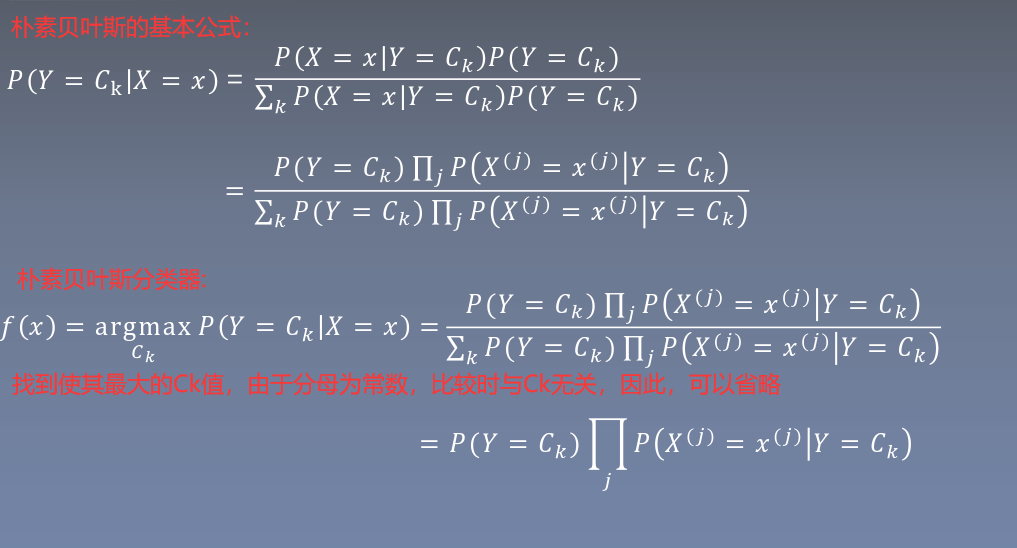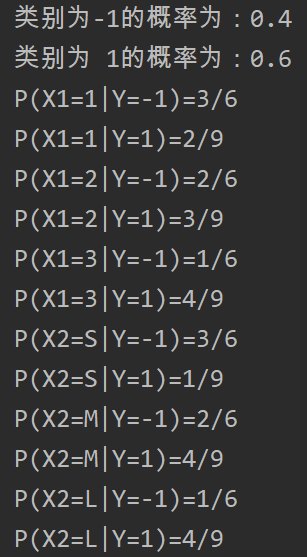（每天一點點）統計學習方法——樸素貝葉斯法

1、概率論基礎

貝葉斯原理就是求解后驗概率。如果已知p(x|c)要求p(c|x)，我們可以使用貝葉斯公式進行求解。
貝葉斯公式：
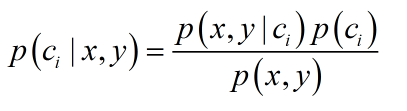
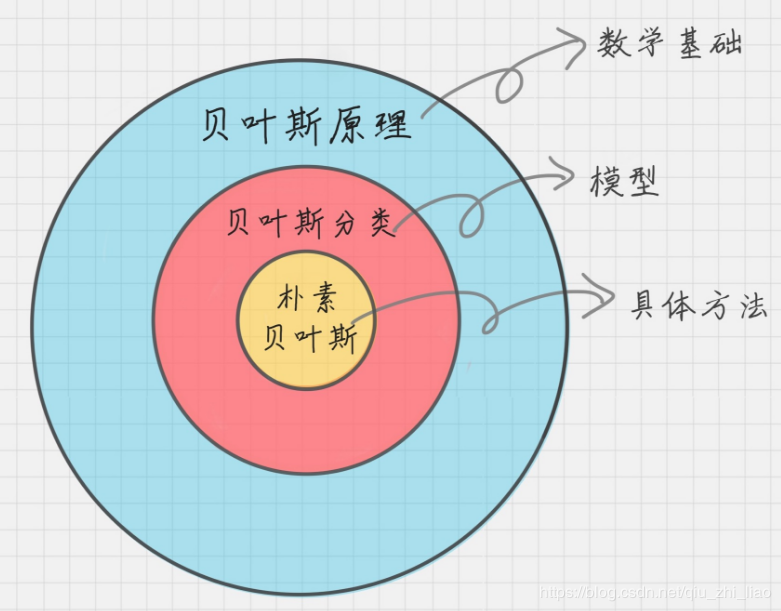
在這里插入圖片描述

ps：圖片出處
樸素貝葉斯分類器中的樸素指的是特征樣本之間相互獨立。

2、舉個栗子

已在線社區留言板為例子，我們要屏蔽侮辱性言論。對此問題我們建立兩個類別：侮辱性和非侮辱性。我們先定一個詞典，比如[dog,love,cute…]，然后把一條留言分成詞向量[0,1,0,0,…1]。其中1代表該詞在詞典里出現過，0代表這個詞沒有出現。比如dog對應0，就說明這個詞沒出現過。

然后我們先通過類別i（侮辱性留言或非侮辱性留言）中文檔數除以總文檔數來計算概率p(ci)。接著我們重寫p(x,y)為p(w),其中w表示這是一向量。
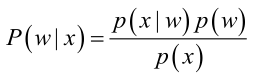
在這里插入圖片描述
用ci（類別）來替換上面式子的x。假設w={w1,w2,w3……}，因為相互獨立，我們就可以把p(w|ci)拆成p(w1|ci)p(w2|ci)p(w3|ci)…即每個單詞在侮辱性留言/非侮辱性留言出現的概率。

最后我們通過貝葉斯公式就可以計算出p(ci|w)，也就是在這個詞向量出現的情況下，可能是侮辱性留言/非侮辱性留言的概率。（兩個都算然后比較概率的大小）

3、極大似然估計

但是在實際問題中并不都是這樣幸運的，我們能獲得的數據可能只有有限數目的樣本數據，而先驗概率和類條件概率(各類的總體分布)都是未知的。根據僅有的樣本數據進行分類時，一種可行的辦法是我們需要先對先驗概率和類條件概率進行估計，然后再套用貝葉斯分類器。

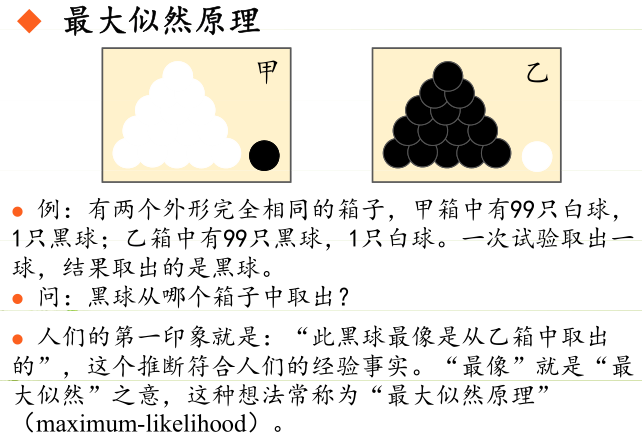
在這里插入圖片描述

極大似然估計提供了一種給定觀察數據來評估模型參數的方法，即：“模型已定，參數未知”。通過若干次試驗，觀察其結果，利用試驗結果得到某個參數值能夠使樣本出現的概率為最大，則稱為極大似然估計。

在樸素貝葉斯法中，學習意味著估計P(Y=ck）和P（X^（j）=x^(j)|Y=ck）我們可以求出先驗概率P（Y=ck）和P(X^(j)=ajl|Y=ck)的極大似然估計。公式分別如下：
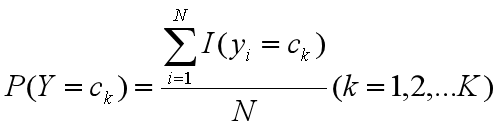
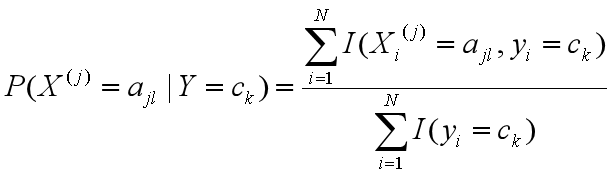
在這里插入圖片描述

在這里插入圖片描述
ps：就是以現有的數據來預測參數。

代碼

#sklearn實例

from sklearn.naive_bayes import GaussianNB

clf = GaussianNB()
clf.fit(X_train, y_train)

clf.predict([[4.4,  3.2,  1.3,  0.2]])
#output:array([0.])

本文鏈接：https://blog.csdn.net/weixin_44254608/article/details/106572873

智能推薦

統計學習方法——第四章樸素貝葉斯

參考網址如下，講解更詳細： http://www.jianshu.com/p/5fd446efefe9 http://blog.csdn.net/v_victor/article/details/51319873 樸素navie：條件獨立性【問題的引入】經典的貝葉斯公式實際問題中，能獲得的數據可能只有有限數...

統計學習方法-代碼實現-樸素貝葉斯

目錄貝葉斯定理樸素貝葉斯算法貝葉斯估計代碼實現貝葉斯定理其中所以樸素貝葉斯分類器為因為分母是一定的，與Y無關，所以簡化為樸素貝葉斯算法貝葉斯估計因為可能為0，則無法計算所以將樸素貝葉斯修正為貝葉斯估計代碼實現...

文章目錄 1.樸素貝葉斯的基本方法 2.樸素貝葉斯的參數估計 1.極大似然估計 2.樸素貝葉斯算法 3.貝葉斯估計 3.后驗概率最大化-期望風險最小化 4.樸素貝葉斯代碼實現 1.樸素貝葉斯的基本方法 2.樸素貝葉斯的參數估計 1.極大似然估計 2.樸素貝葉斯算法 3.貝葉斯估計用極大似然估計可能出現所要估計的概率值為0的情況，這是會影響到后驗概率的計算結果，使分類產生偏差。解決這一問題的方法就...

每天學習一點點

1.box-shadow: 水平位移垂直位移模糊程度顏色 2.calc(): 用于動態計算長度值支持’+’,’-’,’*’,’/'運算 3.transition: 貝塞爾曲線（cubic-bezier）幾個常用的固定值： ease：cubic-bezier(.25, .1, .25, 1) liner：c...

每天一點點(StringBoot 我的第一次)

框架環境: 編譯工具:idea java jdk(1.8) maven 3.3.9 以上點環境需求自己下載安裝即可(百度一坨) 下面的才是關鍵 : 我們有數據源卻沒有配置( 我們在創建項目的時候現在了mybatis + mysql 所以才有這個提示 :先不著急配置&...