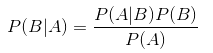一、概率知識點復習

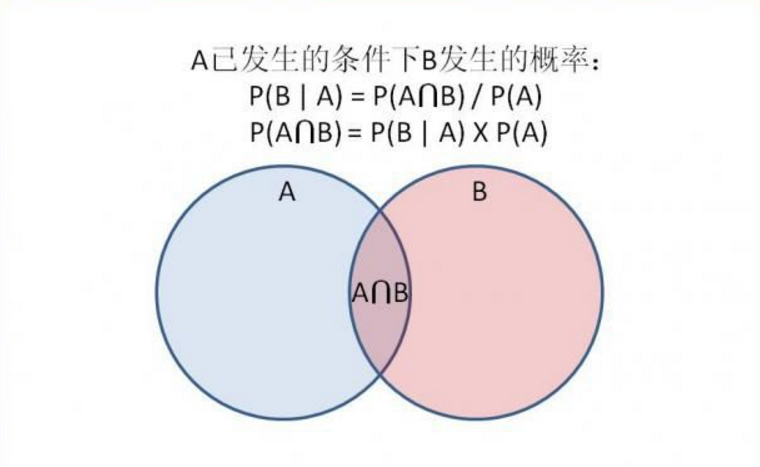
（1）條件概率

就是事件A在另外一個事件B已經發生條件下的發生概率。條件概率表示為P(A|B)，讀作“在B條件下A的概率”。

（2）聯合概率

可以簡單的理解為事件A與事件B都發生的概率，記為P(AB)或P(A, B)。

此處就有  P(A, B) = P(A|B) * P(B)

若事件A與事件B獨立，則有 P(A, B) = P(A) * P(B)，這也說明了此時 P(A|B) = P(A)。

（3）全概率

如果事件B1，B2，B3，…，Bn 構成一個完備事件組，即它們兩兩互不相容，其和為全集；并且P(Bi)大于0，則對任一事件A有：

P(A)=P(A|B1)*P(B1) + P(A|B2)*P(B2) + ... + P(A|Bn)*P(Bn)

（這里我就只介紹這么多，大家如果對全概率不太理解的可以去補充補充！這點很重要，對后面理解貝葉斯很重要！！今天我重點在講貝葉斯，所以此處就不在多講全概率啦~~~后面的例子會涉及到！）

二、貝葉斯定理

我們在生活中經常遇到這種情況：我們可以很容易直接得出P(A|B)，P(B|A)則很難直接得出，但我們更關心P(B|A)，貝葉斯定理就為我們打通從P(A|B)求得P(B|A)的道路。

此處我就給出貝葉斯定理的公式（其推導沒必要知道）

（便于大家記憶，可以這樣記P(A, B) = P(A|B) * P(B) 且P(A, B) = P(B|A) * P(A)，大家將兩式子合并會有P(A|B) * P(B) =  P(B|A) * P(A)）

便于大家記住這個公式在此有必要舉個例子：

現有校準過的槍5把，沒校準過的3把。現在某人用校準過的槍打靶中靶概率為0.8，用沒校準過的槍中靶概率只為0.3。現在已知拿起一把槍打靶中靶了，請問這個槍是校準過的搶的概率？

（分析：直接套用上面的公式，但做P(A)的時候是要用到全概率的！！（全概率的重要性體現出來了~））

                令中靶的事件為A，選中校準過的槍的事件為B1，選中未校準過的搶的事件為B2

                則： P(B1) = 5 / 8        P(B2) = 3 / 8

                         P(A) = P(A|B1)P(B1) + P(A|B2)P(B2) = 49 / 80

                         P(A|B1) = 4 / 5

                上面的都做出來后，你會發現根據貝葉斯定理的公式是不是就可以求出P(B1|A)啦~

                得：      P(B1|A) = P(B1)P(A|B1) / P(A) = 40 / 49

思考：通過這個例子我們可以看到貝葉斯定理的作用，他就是打通了P(A|B1)求得P(B1|A)的道路，也可清晰理解到貝葉斯定理用來可分類！！

三、簡聊貝葉斯網絡

此章節只是為了讓大家能看懂簡單的貝葉斯網絡圖就ok~

貝葉斯網絡，由一個有向無環圖(DAG)和條件概率表(CPT)組成。 貝葉斯網絡通過一個有向無環圖來表示一組隨機變量跟它們的條件依賴關系。它通過條件概率分布來參數化。每一個結點都通過P(node|Pa(node))來參數化，Pa(node)表示網絡中的父節點。

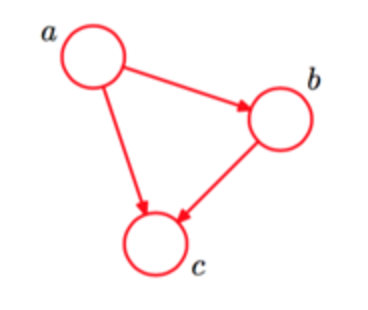
如下圖是一個簡單的貝葉斯網絡
                                 

其對應的全概率公式為：

P(a,b,c)=P(c∣a,b)P(b∣a)P(a)P(a,b,c)=P(c∣a,b)P(b∣a)P(a)

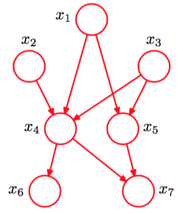
較復雜的貝葉斯網絡
                           

其對應的全概率公式為：

P(x1,x2,x3,x4,x5,x6,x7)=P(x1)P(x2)P(x3)P(x4∣x1,x2,x3)P(x5∣x1,x3)P(x6∣x4)P(x7∣x4,x5)

注意關系：一事件只與其父事件相關！！

四、樸素貝葉斯分類

樸素貝葉斯分類是一種十分簡單的分類算法，叫它樸素貝葉斯分類是因為這種方法的思想真的很樸素，樸素貝葉斯的思想基礎是這樣的：對于給出的待分類項，求解在此項出現的條件下各個類別出現的概率，哪個最大，就認為此待分類項屬于哪個類別。通俗來說，就好比這么個道理，你在街上看到一個黑人，我問你你猜這哥們哪里來的，你十有八九猜非洲。為什么呢？因為黑人中非洲人的比率最高，當然人家也可能是美洲人或亞洲人，但在沒有其它可用信息下，我們會選擇條件概率最大的類別，這就是樸素貝葉斯的思想基礎。

樸素貝葉斯分類的正式定義如下：

1、設為一個待分類項，而每個a為x的一個特征屬性。

2、有類別集合。

3、計算。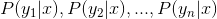

4、如果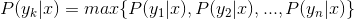，則。

那么現在的關鍵就是如何計算第3步中的各個條件概率。我們可以這么做：

1、找到一個已知分類的待分類項集合，這個集合叫做訓練樣本集。

2、統計得到在各類別下各個特征屬性的條件概率估計。即：

。

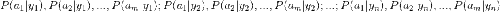3、如果各個特征屬性是條件獨立的，則根據貝葉斯定理有如下推導：

      

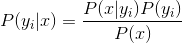
 因為分母對于所有類別為常數，因為我們只要將分子最大化皆可。又因為各特征屬性是條件獨立的，所以有：

      

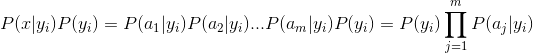
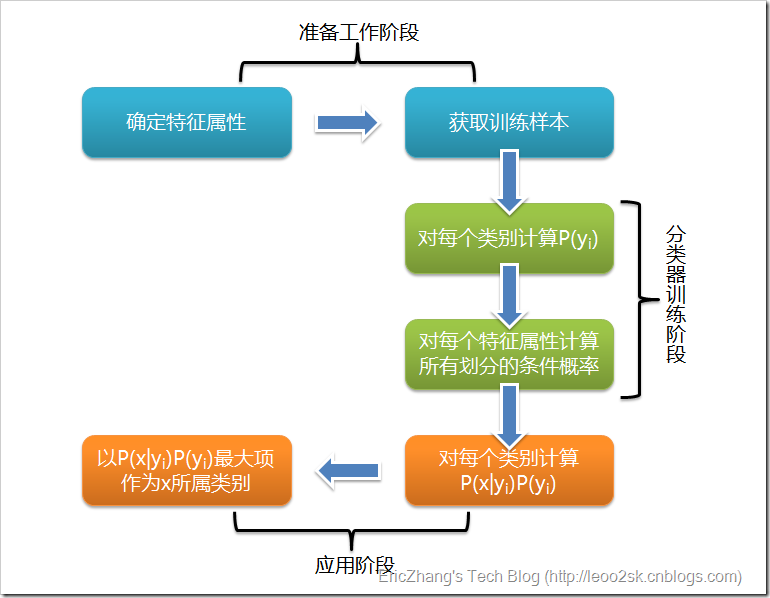
根據上述分析，樸素貝葉斯分類的流程可以由下圖表示（暫時不考慮驗證）：

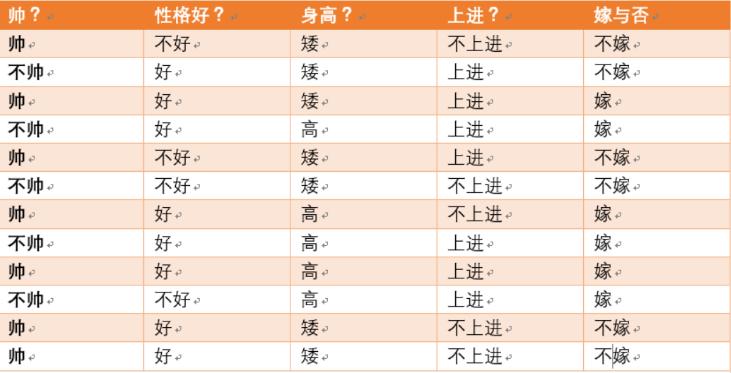
五、樸素貝葉斯分類實例

      下面討論一個使用樸素貝葉斯分類解決實際問題的例子，為了簡單起見，對例子中的數據做了適當的簡化。

      這個問題是這樣的，對于SNS社區來說，不真實賬號（使用虛假身份或用戶的小號）是一個普遍存在的問題，作為SNS社區的運營商，希望可以檢測出這些不真實賬號，從而在一些運營分析報告中避免這些賬號的干擾，亦可以加強對SNS社區的了解與監管。

      如果通過純人工檢測，需要耗費大量的人力，效率也十分低下，如能引入自動檢測機制，必將大大提升工作效率。這個問題說白了，就是要將社區中所有賬號在真實賬號和不真實賬號兩個類別上進行分類，下面我們一步一步實現這個過程。

      首先設C=0表示真實賬號，C=1表示不真實賬號。

      1、確定特征屬性及劃分

      這一步要找出可以幫助我們區分真實賬號與不真實賬號的特征屬性，在實際應用中，特征屬性的數量是很多的，劃分也會比較細致，但這里為了簡單起見，我們用少量的特征屬性以及較粗的劃分，并對數據做了修改。

      我們選擇三個特征屬性：a1：日志數量/注冊天數，a2：好友數量/注冊天數，a3：是否使用真實頭像。在SNS社區中這三項都是可以直接從數據庫里得到或計算出來的。

      下面給出劃分：a1：{a<=0.05, 0.05<a<0.2, a>=0.2}，a1：{a<=0.1, 0.1<a<0.8, a>=0.8}，a3：{a=0（不是）,a=1（是）}。

      2、獲取訓練樣本

      這里使用運維人員曾經人工檢測過的1萬個賬號作為訓練樣本。

      3、計算訓練樣本中每個類別的頻率

      用訓練樣本中真實賬號和不真實賬號數量分別除以一萬，得到：

      

      

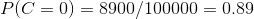
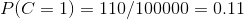
      4、計算每個類別條件下各個特征屬性劃分的頻率

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

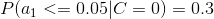
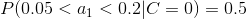
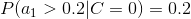
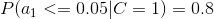
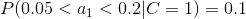
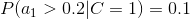
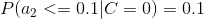
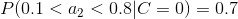
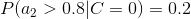
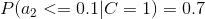
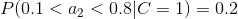
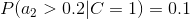
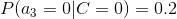
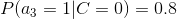
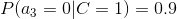
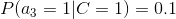
      5、使用分類器進行鑒別

      下面我們使用上面訓練得到的分類器鑒別一個賬號，這個賬號使用非真實頭像，日志數量與注冊天數的比率為0.1，好友數與注冊天數的比率為0.2。

      

      

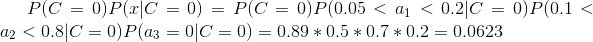
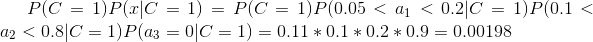
      可以看到，雖然這個用戶沒有使用真實頭像，但是通過分類器的鑒別，更傾向于將此賬號歸入真實賬號類別。這個例子也展示了當特征屬性充分多時，樸素貝葉斯分類對個別屬性的抗干擾性。

六、三種常見的樸素貝葉斯模型

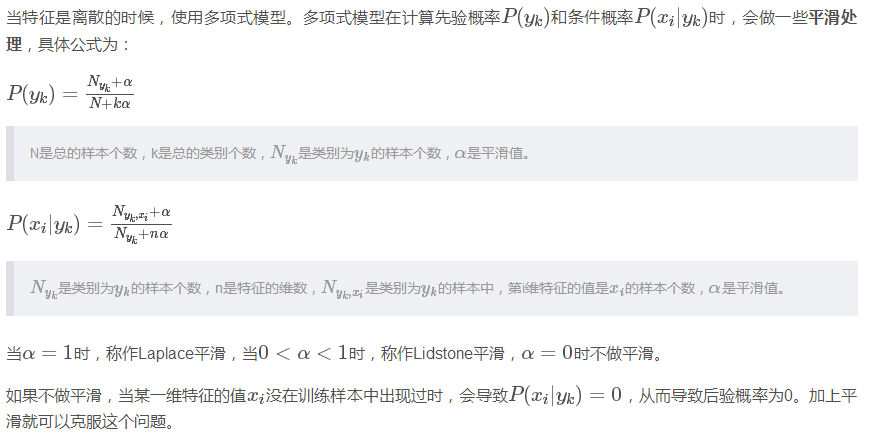
1. 多項式模型

2. 高斯模型

當特征是連續變量的時候，運用多項式模型就會導致很多P(xi|yk)=0P(xi|yk)=0（不做平滑的情況下），此時即使做平滑，所得到的條件概率也難以描述真實情況。所以處理連續的特征變量，應該采用高斯模型。

高斯模型假設每一維特征都服從高斯分布（正態分布）：

3. 伯努利模型

與多項式模型一樣，伯努利模型適用于離散特征的情況，所不同的是，伯努利模型中每個特征的取值只能是1和0(以文本分類為例，某個單詞在文檔中出現過，則其特征值為1，否則為0)。

 

七、樸素貝葉斯的優缺點

樸素貝葉斯的主要優點有：

　　　　1）樸素貝葉斯模型發源于古典數學理論，有穩定的分類效率。

　　　　2）對小規模的數據表現很好，能個處理多分類任務，適合增量式訓練，尤其是數據量超出內存時，我們可以一批批的去增量訓練。

　　　　3）對缺失數據不太敏感，算法也比較簡單，常用于文本分類。

        4）不存在過擬合的說法。

　　　　樸素貝葉斯的主要缺點有：　　　

　　　　1） 理論上，樸素貝葉斯模型與其他分類方法相比具有最小的誤差率。但是實際上并非總是如此，這是因為樸素貝葉斯模型給定輸出類別的情況下,假設屬性之間相互獨立，這個假設在實際應用中往往是不成立的，在屬性個數比較多或者屬性之間相關性較大時，分類效果不好。而在屬性相關性較小時，樸素貝葉斯性能最為良好。對于這一點，有半樸素貝葉斯之類的算法通過考慮部分關聯性適度改進。

　　　　2）需要知道先驗概率，且先驗概率很多時候取決于假設，假設的模型可以有很多種，因此在某些時候會由于假設的先驗模型的原因導致預測效果不佳。

　　　　3）由于我們是通過先驗和數據來決定后驗的概率從而決定分類，所以分類決策存在一定的錯誤率。

　　　　4）對輸入數據的表達形式很敏感。

 

主要參考博客:

（1）張洋： http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html

（2） https://blog.csdn.net/u012162613/article/details/48323777