監督式機器學習

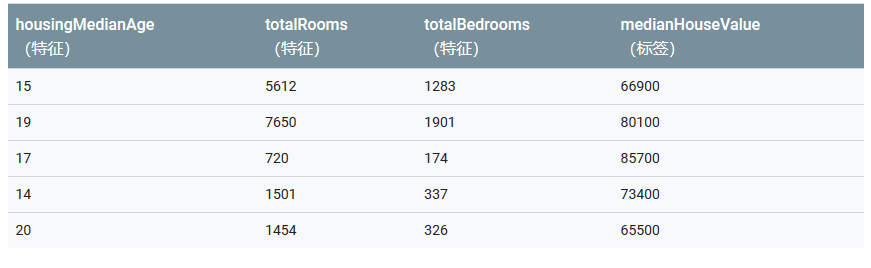
標簽： 指我們要預測的真實事物——y（ 基本線性回歸(也叫簡單線性回歸)中的 y 變量 ）,可以簡單理解為模型的預測結果

特征： 指用于描述數據的輸入變量 —— xi （ 基本線性回歸中的 {x1、x2、…xn} 變量 ），簡單的機器學習項目可能會使用單個特征，而比較復雜的機器學習項目可能會使用數百萬個特征 【 合適的特征應該是具體且可量化的 】

樣本： 是指數據的特定實例——x

? 有標簽樣本 同時包含特征和標簽 ：labeled examples: {features, label}: (x, y)， 使用有標簽樣本來訓練模 型

? 無標簽樣本具有 {特征, ?}：(x, ?) ， 用于對新數據做出預測

? 在使用有標簽樣本訓練模型之后，我們會使用該模型預測無標簽樣本的標簽

模型可將樣本映射到預測標簽（ 模型定義了特征與標簽之間的關系 ）：y’ ，所謂模型就是執行預測的工具，由模型的內部參數定義，這些內部參數值是通過學習得到的 ，通過學習規律來嘗試創建模型，從而通過模型預測標簽

	**訓練**是指創建或**學習**模型。也就是說，向模型展示有標簽樣本，讓模型逐漸學習特征與標簽之間的關系。 

? 推斷是指將訓練后的模型應用于無標簽樣本。也就是說，使用經過訓練的模型做出有用的預測 (y')

回歸模型可預測連續值 ， 分類模型可預測離散值 。

線性回歸、訓練和損失

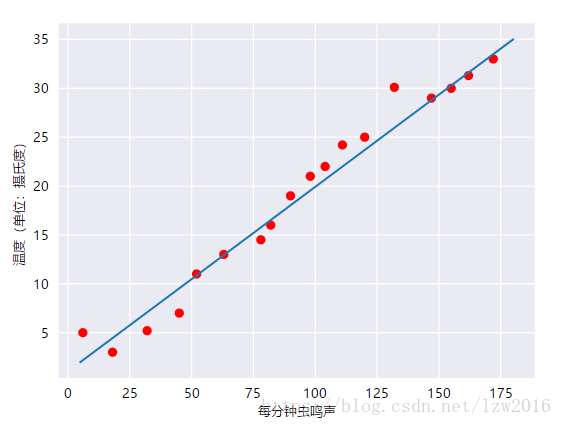
$y = mx + b$y=mx+b ，y 是我們試圖預測的值 ，m 指的是直線的斜率 ，x 即輸入特征的值 ， b指的是 y 軸截距 。

模型方程式 :$y' = w1x1 + b$y′=w1x1+b,

y’指的是預測標簽（理想輸出值） ， b指的是偏差（y 軸截距）。而在一些機器學習文檔中，它稱為 w0。

w1 指的是特征 1 的權重。 x1 指的是特征（已知輸入項）。

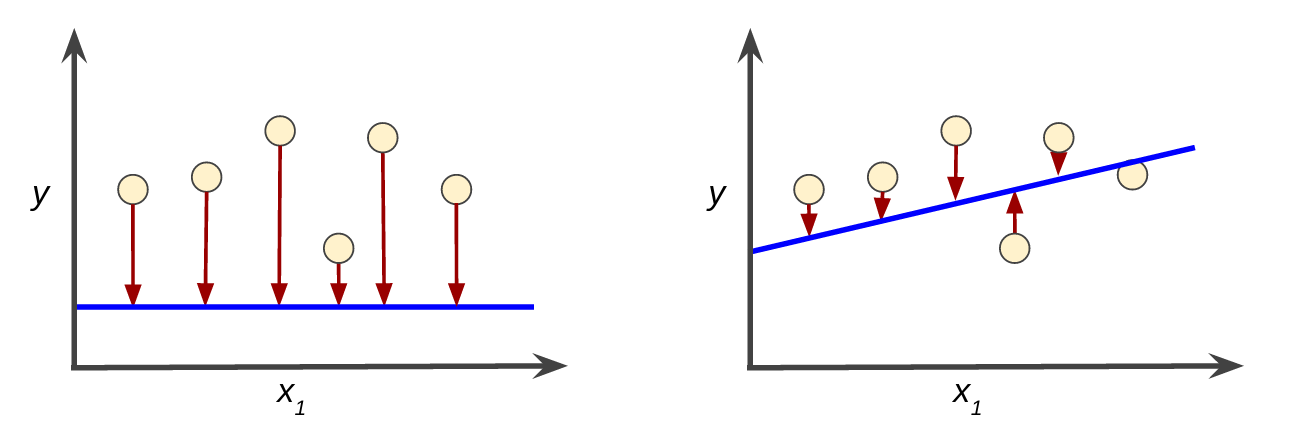
訓練模型表示通過有標簽樣本來學習（確定）所有權重和偏差的理想值。在監督式學習中，機器學習算法通過以下方式構建模型：檢查多個樣本并嘗試找出可最大限度地減少損失的模型；這一過程稱為經驗風險最小化。

損失是一個數值，表示對于單個樣本而言模型預測的準確程度 。即單個樣本的真正標簽與模型的預測標簽的差距。 如果模型的預測完全準確，則損失為零，否則損失會較大。訓練模型的目標是從所有樣本中找到一組平均損失“較小”的權重和偏差。

平方損失（又稱為 L2 損失）的損失函數

  = the square of the difference between the label and the prediction
  = (observation - prediction(x))2
  = (y - y')2

均方誤差 (MSE) 指的是每個樣本的平均平方損失。要計算 MSE，請求出各個樣本的所有平方損失之和，然后除以樣本數量：

[外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳(img-mpHnR3mf-1572745710789)(G:\Mypdf\markdown\2019-10-26_092758.jpg)]

x指的是模型進行預測時使用的特征集 ，y 指的是樣本的標簽 ，prediction(x)指的是權重和偏差與特征集 x 結合的函數。D指的是包含多個有標簽樣本（即 (x,y)）的數據集。 N 指的是 D 中的樣本數量。

迭代方式降低損失

“模型”部分將一個或多個特征作為輸入，然后返回一個預測 (y’) 作為輸出。 對于線性回歸問題，事實證明初始值并不重要。我們可以隨機選擇值，不過我們還是選擇采用以下這些無關緊要的值：b = 0，w1 = 0。

“計算損失”部分是模型將要使用的損失函數。

“計算參數更新”部分。機器學習系統就是在此部分檢查損失函數的值，并為差距(b)和權重(w1,w2,w3……wn)生成新值。現在，假設這個神秘的綠色框會產生新值，然后機器學習系統將根據所有標簽重新評估所有特征,為損失函數生成一個新值，而該值又產生新的參數值。這種學習過程會持續迭代，直到該算法發現損失可能最低的模型參數。 可以不斷迭代，直到總體損失不再變化或至少變化極其緩慢為止。這時候，我們可以說該模型已收斂。

降低損失 (Reducing Loss)：梯度下降法

回歸問題產生的損失與權重圖為凸形

凸形問題只有一個最低點；即只存在一個斜率正好為 0 的位置。這個最小值就是損失函數收斂之處。

梯度下降法的第一個階段是為 w1 選擇一個起始值（起點）。起點并不重要；因此很多算法就直接將 w1 設為 0 或隨機選擇一個值。 然后，梯度下降法算法會計算損失曲線在起點處的梯度。簡而言之，梯度是偏導數的矢量；它可以讓您了解哪個方向距離目標“更近”或“更遠”。

偏導數

多變量函數指的是具有多個參數的函數，例如：
$f(x,y)=e^2y sin(x)$f(x,y)=e2ysin(x)
f 相對于 x 的偏導數表示：
$?f/?x$?f/?x
是 f (x) 的導數。要計算以下值：
$?f/?x$?f/?x
您必須使 y 保持固定不變（因此 f 現在是只有一個變量 x 的函數）,即假設y為常量，然后取 f 相對于 x 的常規導數。【高等數學中偏導數的求法】

函數的梯度是偏導數相對于所有自變量的矢量，表示如下：
$?f$?f
梯度是一個矢量，因此具有以下兩個特征：方向、大小

$?f = (?f/?x,?f/?y,?f/?z) = ?f/?x*i + ?f/?y*j + ?f/?z*k$?f=(?f/?x,?f/?y,?f/?z)=?f/?x?i+?f/?y?j+?f/?z?k

i, j, k 為標準的單位向量，分別指向 x, y 跟 z 坐標的方向。

梯度始終指向損失函數中增長最為迅猛的方向,梯度下降法依賴于負梯度 。梯度下降法算法會沿著負梯度的方向走一步，以便盡快降低損失。 **走一個梯度步長將我們移動到損失曲線上的下一個點。**然后，梯度下降法會重復此過程，逐漸接近最低點。

那么問題在于每次走多大的步長合適呢？這就涉及到了學習效率的內容：

梯度矢量具有方向和大小。梯度下降法算法用梯度乘以一個稱為學習速率（有時也稱為步長）的標量，以確定下一個點的位置。 超參數是編程人員在機器學習算法中用于調整的旋鈕。大多數機器學習編程人員會花費相當多的時間來調整學習速率 。

隨機梯度下降法

在梯度下降法中，批量指的是用于在單次迭代中計算梯度的樣本總數。 包含隨機抽樣樣本的大型數據集可能包含冗余數據。實際上，批量大小越大，出現冗余的可能性就越高。一些冗余可能有助于消除雜亂的梯度，但超大批量所具備的預測價值往往并不比大型批量高。

通過從我們的數據集中隨機選擇樣本，我們可以通過小得多的數據集估算（盡管過程非常雜亂）出較大的平均值。 隨機梯度下降法 (SGD) 將這種想法運用到極致，它每次迭代只使用一個樣本（批量大小為 1）。如果進行足夠的迭代，SGD 也可以發揮作用，但過程會非常雜亂。“隨機”這一術語表示構成各個批量的一個樣本都是隨機選擇的。 小批量隨機梯度下降法（小批量 SGD）是介于全批量迭代與 SGD 之間的折衷方案。小批量通常包含 10-1000 個隨機選擇的樣本。小批量 SGD 可以減少 SGD 中的雜亂樣本數量，但仍然比全批量更高效。

使用TensorFlow

基于圖表的計算框架

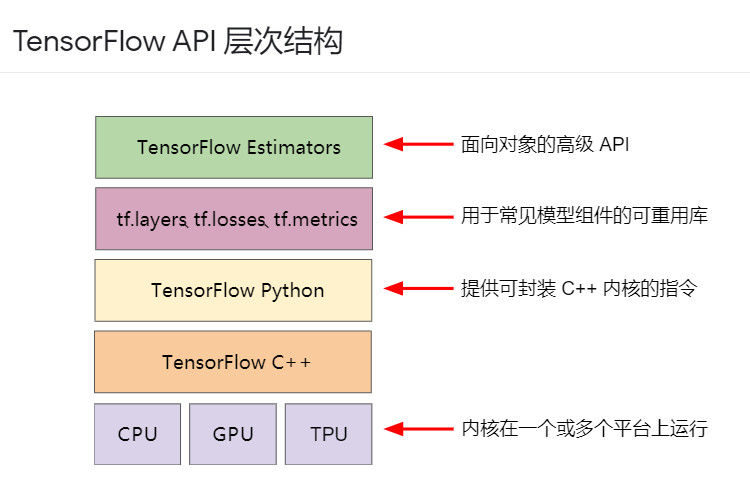
工具包 說明

Estimator (tf.estimator)	高級 OOP API。
tf.layers/tf.losses/tf.metrics	用于常見模型組件的庫。
TensorFlow	低級 API

TensorFlow 由以下兩個組件組成：

• 圖協議緩沖區
• 執行（分布式）圖的運行時

這兩個組件類似于 Java 編譯器和 JVM。正如 JVM 會實施在多個硬件平臺（CPU 和 GPU）上一樣，TensorFlow 也是如此。

泛化

泛化是指模型很好地擬合以前未見過的新數據（從用于創建該模型的同一分布中抽取）的能力。

過擬合： 為了得到一致假設而使假設變得過度嚴格稱為過擬合。

過擬合是由于模型的復雜程度超出所需程度而造成的。機器學習的基本沖突是適當擬合我們的數據，但也要盡可能簡單地擬合數據。機器學習的目標是對從真實概率分布（已隱藏）中抽取的新數據做出良好預測。 機器學習模型旨在根據以前未見過的新數據做出良好預測 。

一種方法是將您的數據集分成兩個子集：

• 訓練集 - 用于訓練模型的子集。

• 測試集 - 用于測試訓練后模型的子集 。

  一般來說，在測試集上表現是否良好是衡量能否在新數據上表現良好的有用指標，前提是：

  • 測試集足夠大。

  • 您不會反復使用相同的測試集來作假。

訓練集和測試集

確保您的測試集滿足以下兩個條件：

• 規模足夠大，可產生具有統計意義的結果。
• 能代表整個數據集。換言之，挑選的測試集的特征應該與訓練集的特征相同。

請勿對測試數據進行訓練

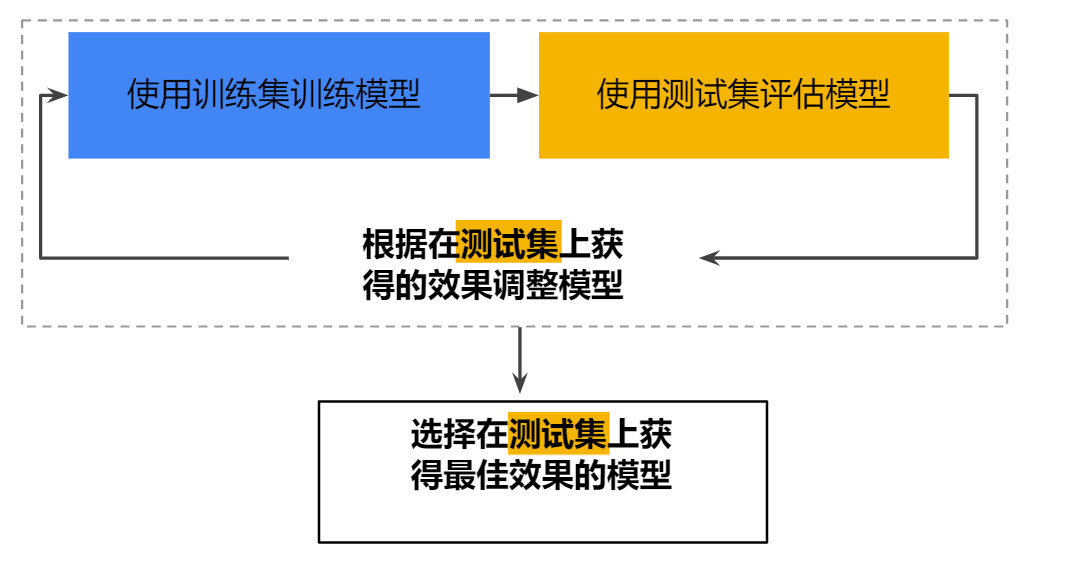
但是這種模型挑戰會大大提高過擬合的概率。

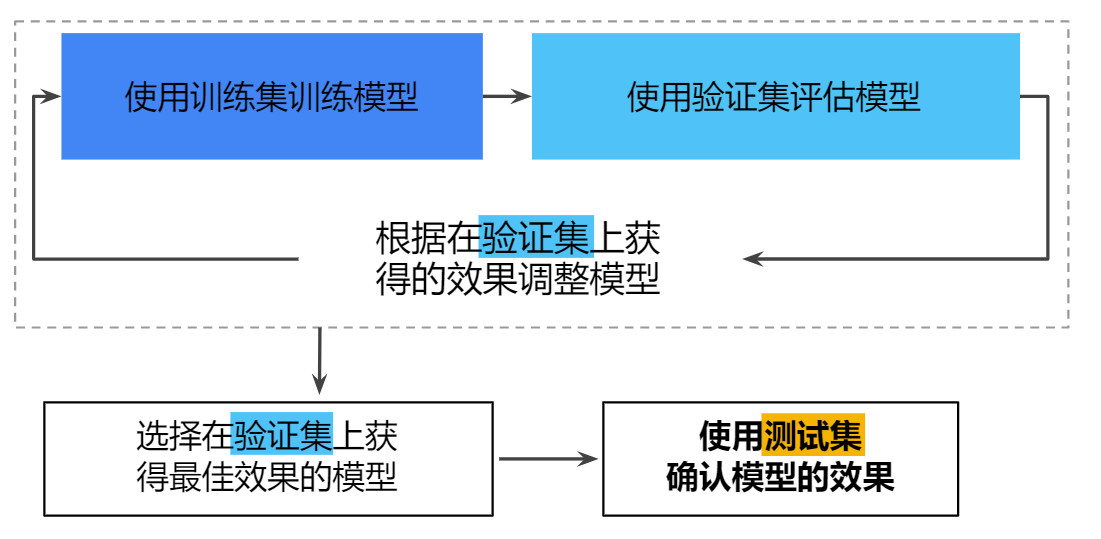
驗證集

通過將數據集劃分為三個子集，可以大幅降低過擬合的發生幾率 。 將單個數據集劃分為三個子集：訓練集、測試集、驗證集， 在模型“通過”驗證集之后，使用測試集再次檢查評估結果 。

表示

特征工程

機器學習項目中，關注點是特征表示。也就是說，開發者通過添加和改善特征來調整模型。

將原始數據映射到特征

特征工程指的是將原始數據轉換為特征矢量。 進行特征工程預計需要大量時間。(大約75%)

許多機器學習模型都必須將特征表示為實數向量，因為特征值必須與模型權重相乘。

映射數值： 整數和浮點數據不需要特殊編碼 ，直接轉化為特征向量就可以和權重相乘。

映射分類值： 分類特征可能具有一組離散的值。

模型不能將字符串與學習到的權重相乘，因此我們使用特征工程將字符串轉換為數字值。

可以定義一個從特征值（我們將其稱為可能值的詞匯表）到整數的映射。世界上的每條街道并非都會出現在我們的數據集中，因此我們可以將所有其他街道分組為一個全部包羅的**“其他”類別**，稱為 OOV（詞匯表外）分桶 。

向量(特征向量)的長度等于詞匯表中的元素數。當只有一個值為 1 時，這種表示法稱為獨熱編碼 。 當有多個值為 1 時，這種表示法稱為多熱編碼。

通過獨熱編碼映射街道地址。

該方法能夠有效地為每個特征值（例如，街道名稱）創建布爾變量。采用這種方法時，如果房屋位于 Shorebird Way 街道上，則只有 Shorebird Way 的二元值為 1。因此，該模型僅使用 Shorebird Way 的權重。同樣，如果房屋位于兩條街道的拐角處，則將兩個二元值設為 1，并且模型將使用它們各自的權重。

稀疏表示法： 其中僅存儲非零值。在稀疏表示法中，仍然為每個特征值學習獨立的模型權重

良好特征的特點

盡量少使用出現次數少的離散特征值，良好的特征值應該在數據集中出現大約 5 次以上。這樣一來，模型就可以學習該特征值與標簽是如何關聯的。也就是說，大量離散值相同的樣本可讓模型有機會了解不同設置中的特征，從而判斷何時可以對標簽很好地做出預測。相反，如果某個特征的值僅出現一次或者很少出現，則模型就無法根據該特征進行預測。最好具有清晰明確的含義

每個特征對于項目中的任何人來說都應該具有清晰明確的含義。

實際數據內不要摻入特殊值， 良好的浮點特征不包含超出范圍的異常斷點或特殊的值 。為解決特殊值的問題，需將該特征轉換為兩個特征：

• 一個特征只存儲正常的特征值，不含特殊值。
• 一個特征存儲布爾值，表示是否提供了正確的特征值。為該布爾值特征指定一個名稱。

考慮上游不穩定性，特征的定義不應隨時間發生變化。

清理數據

縮放特征值

縮放是指將浮點特征值從自然范圍（例如 100 到 900）轉換為標準范圍（例如 0 到 1 或 -1 到 +1）。

如果特征集包含多個特征，則縮放特征可以帶來以下優勢：

• 幫助梯度下降法更快速地收斂。
• 幫助避免“NaN 陷阱”。在這種陷阱中，模型中的一個數值變成 NaN（例如，當某個值在訓練期間超出浮點精確率限制時），并且模型中的所有其他數值最終也會因數學運算而變成 NaN。
• 幫助模型為每個特征確定合適的權重。如果沒有進行特征縮放，則模型會對范圍較大的特征投入過多精力。

要縮放數字數據，一種顯而易見的方法是將 [最小值，最大值] 以線性方式映射到較小的范圍，例如 [-1，+1]。

另一種熱門的縮放策略是計算每個值的 Z 得分。Z 得分與距離均值的標準偏差數相關。換而言之：
$scaledvalue=(value?mean)/stddev$scaledvalue=(value?mean)/stddev
scaledvalue：縮放結果 value：原始值 mean：均值 stddev：標準偏差數

處理極端離群值

1. 一種方法是對每個值取對數 ， 對數縮放可稍稍緩解這種影響 ，但最終結果仍有一些較大的離群值
2. 對特征值進行限定，所有超過限定的特征值都將變成最大特征值。

分箱

原因：特征值和標簽之間不存在線性關系，將特征值分為若干個部分，每個部分存在線性關系，分箱之后，我們的模型現在可以為每個部分學習完全不同的權重 。

清查

在現實生活中，數據集中的很多樣本是不可靠的，原因有以下一種或多種：

• 遺漏值。 例如，有人忘記為某個房屋的年齡輸入值。
• 重復樣本。 例如，服務器錯誤地將同一條記錄上傳了兩次。
• 不良標簽。 例如，有人錯誤地將一顆橡樹的圖片標記為楓樹。
• 不良特征值。 例如，有人輸入了多余的位數，或者溫度計被遺落在太陽底下。

一旦檢測到存在這些問題，您通常需要將相應樣本從數據集中移除，從而“修正”不良樣本。 要檢測遺漏值、重復樣本、 不良特征值或標簽 ，您可以編寫一個簡單的程序來進行過濾或修正。 除了檢測各個不良樣本之外，您還必須檢測集合中的不良數據 。

特征組合

特征組合是指兩個或多個特征相乘形成的合成特征 。 特征的相乘組合可以提供超出這些特征單獨能夠提供的預測能力。

特征組合是指通過將兩個或多個輸入特征相乘來對特征空間中的非線性規律進行編碼的合成特征。

特征組合的種類

我們可以創建很多不同種類的特征組合。例如：

• [A X B]：將兩個特征的值相乘形成的特征組合。
• [A x B x C x D x E]：將五個特征的值相乘形成的特征組合。
• [A x A]：對單個特征的值求平方形成的特征組合。

通過采用隨機梯度下降法，可以有效地訓練線性模型。

組合獨熱矢量

機器學習模型經常組合獨熱特征矢量，將獨熱特征矢量的特征組合視為邏輯連接 。

假設您對緯度和經度進行分箱，獲得單獨的獨熱 5 元素特征矢量。例如，指定的緯度和經度可以表示如下：

binned_latitude = [0, 0, 0, 1, 0] //緯度
binned_longitude = [0, 1, 0, 0, 0] //經度

假設您對這兩個特征矢量創建了特征組合：

binned_latitude X binned_longitude

此特征組合是一個 25 元素獨熱矢量（24 個 0 和 1 個 1）。該組合中的單個 1 表示緯度與經度的特定連接。然后，您的模型就可以了解到有關這種連接的特定關聯性。

線性學習器可以很好地擴展到大量數據。對大規模數據集使用特征組合是學習高度復雜模型的一種有效策略。

簡化正則化

正則化指的是降低模型的復雜度以減少過擬合 。

現象起因： 某個模型的訓練損失逐漸減少，但驗證損失最終增加。換言之，該泛化曲線顯示該模型與訓練集中的數據過擬合。

也就是說，并非只是以最小化損失（經驗風險最小化）為目標：
$minimize(Loss(Data|Model))$minimize(Loss(Data∣Model))
而是以最小化損失和復雜度為目標，這稱為結構風險最小化：
$minimize(Loss(Data|Model) + complexity(Model))$minimize(Loss(Data∣Model)+complexity(Model))
現在，我們的訓練優化算法是一個由兩項內容組成的函數：一個是損失項，用于衡量模型與數據的擬合度，另一個是正則化項，用于衡量模型復雜度。

兩種衡量模型復雜度的常見方式（這兩種方式有些相關）：

• 將模型復雜度作為模型中所有特征的權重的函數。
• 將模型復雜度作為具有非零權重的特征總數的函數。

如果模型復雜度是權重的函數，則特征權重的絕對值越高，對模型復雜度的貢獻就越大。

可以使用 L2 正則化公式來量化復雜度，該公式將正則化項定義為所有特征權重的平方和：

在這個公式中，接近于 0 的權重對模型復雜度幾乎沒有影響，而離群值權重則可能會產生巨大的影響。

lambda

模型開發者通過以下方式來調整正則化項的整體影響：用正則化項的值乘以名為 lambda（又稱為正則化率）的標量 。通過以下計算：
$minimize(Loss(Data|Model) + λcomplexity(Model))$minimize(Loss(Data∣Model)+λcomplexity(Model))
執行 L2 正則化對模型具有以下影響

• 使權重值接近于 0（但并非正好為 0）
• 使權重的平均值接近于 0，且呈正態（鐘形曲線或高斯曲線）分布。

在選擇lambda值時，目的是在簡化模型和訓練數據擬合之間達到適當的平衡：

• 如果您的 lambda 值過高，則模型會非常簡單，但是您將面臨數據欠擬合的風險。您的模型將無法從訓練數據中獲得足夠的信息來做出有用的預測。
• 如果您的 lambda 值過低，則模型會比較復雜，并且您將面臨數據過擬合的風險。您的模型將因獲得過多訓練數據特點方面的信息而無法泛化到新數據。

邏輯回歸

計算概率

許多問題需要將概率估算值作為輸出 。 邏輯回歸是一種極其高效的概率計算機制

通常可以以下兩種方式之一使用返回的概率：

• “按原樣”
• 轉換成二元類別。

邏輯回歸模型如何確保輸出值始終落在 0 和 1 之間。S 型函數生成的輸出值正好具有這些特性。

其定義如下：
$y=1/(1+e^-Z))$y=1/(1+e?Z))
S 型函數會產生以下曲線圖：

[外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳(img-2MvwbA7p-1572745710803)(G:\Mypdf\markdown\2019-10-27_143558.jpg)]

如果z表示使用邏輯回歸訓練的模型的線性層的輸出，則 S 型(z) 函數會生成一個介于 0 和 1 之間的值（概率）

其中：

• y’ 是邏輯回歸模型針對特定樣本的輸出。
• z 是 b + w1x1 + w2x2 + … wNxN
  • w 的值是該模型學習的權重，b 是偏差。
  • x 的值是特定樣本的特征值。

邏輯回歸的損失函數

線性回歸的損失函數是平方損失。邏輯回歸的損失函數是對數損失函數，定義如下：
$LogLoss=∑(x,y)∈D?ylog(y′)?(1?y)log(1?y′)$LogLoss=∑(x,y)∈D?ylog(y′)?(1?y)log(1?y′)
其中：

• (x**y)?D 是包含很多有標簽樣本 (x,y) 的數據集。
• “ y ”是有標簽樣本中的標簽。由于這是邏輯回歸，因此“y”的每個值必須是 0 或 1。
• “ y’ ”是對于特征集“x”的預測值（介于 0 和 1 之間）。

實際上，最大限度地降低損失函數的值會生成最大的似然估計值。

邏輯回歸中的正則化

正則化在邏輯回歸建模中極其重要。如果沒有正則化，邏輯回歸的漸近性會不斷促使損失在高維度空間內達到 0。因此，大多數邏輯回歸模型會使用以下兩個策略之一來降低模型復雜性：

• L2 正則化。

• 早停法，即，限制訓練步數或學習速率。

分類

閾值

為了將邏輯回歸值映射到二元類別，您必須指定分類閾值（也稱為判定閾值）。如果值高于該閾值，則表示“垃圾郵件”；如果值低于該閾值，則表示“非垃圾郵件” 。 閾值取決于具體問題，因此必須對其進行調整。

真與假以及正類別與負類別

正類別和負類別可以粗解為理想情況和不理想情況，其實就是兩種相反的情況，可以自然規定。

真正例是指模型將正類別樣本正確地預測為正類別。同樣，真負例是指模型將負類別樣本正確地預測為負類別。

假正例是指模型將負類別樣本錯誤地預測為正類別，而假負例是指模型將正類別樣本錯誤地預測為負類別。

準確率

準確率是一個用于評估分類模型的指標。通俗來說，準確率是指我們的模型預測正確的結果所占的比例。正式點說，準確率的定義如下：(正確預測數量 / 總預測數量)
$Accuracy=Number of correct predictions / Total number of predictions$Accuracy=Numberofcorrectpredictions/Totalnumberofpredictions
對于二元分類，也可以根據正類別和負類別按如下方式計算準確率：
$Accuracy=(TP+TN) / (TNTP+TN+FP+FN)$Accuracy=(TP+TN)/(TNTP+TN+FP+FN)
其中，TP = 真正例，TN = 真負例，FP = 假正例，FN = 假負例。

當使用分類不平衡的數據集（比如正類別標簽和負類別標簽的數量之間存在明顯差異）時，單單準確率一項并不能反映全面情況 。

精確率和召回率

精確率：在被識別為正類別的樣本中，確實為正類別的比例

定義：
$Precision = TP / (TP + FP)$Precision=TP/(TP+FP)
如果模型的預測結果中沒有假正例，則模型的精確率為 1.0。

召回率 ： 在所有正類別樣本中，被正確識別為正類別的比例

定義：
$召回率 = TP / (TP+FN)$召回率=TP/(TP+FN)
要全面評估模型的有效性，必須同時檢查精確率和召回率。 精確率和召回率往往是此消彼長的情況 。

ROC 和曲線下面積

ROC 曲線（接收者操作特征曲線）是一種顯示分類模型在所有分類閾值下的效果的圖表。 ROC 曲線用于繪制采用不同分類閾值時的 TPR 與 FPR。 該曲線繪制了以下兩個參數：

• 真正例率(TPP True Positive Rate)
• 假正例率(False Positive Rate)

曲線下面積表示“ROC 曲線下面積”。也就是說，曲線下面積測量的是從 (0,0) 到 (1,1) 之間整個 ROC 曲線以下的整個二維面積 。

曲線下面積對所有可能的分類閾值的效果進行綜合衡量。曲線下面積的一種解讀方式是看作模型將某個隨機正類別樣本排列在某個隨機負類別樣本之上的概率。

曲線下面積的取值范圍為 0-1。預測結果 100% 錯誤的模型的曲線下面積為 0.0；而預測結果 100% 正確的模型的曲線下面積為 1.0。

AUC是一個模型評價指標，只能用于二分類模型的評價 。 AUC是Area under curve的首字母縮寫，字面理解就是ROC曲面下面積。

將給定模型的所有預測結果都乘以 統一倍數， AUC 衡量的模型效果 不會發生變化。AUC 以相對預測為依據，因此保持相對排名的任何預測變化都不會對 AUC 產生影響。

預測偏差

邏輯回歸預測應當無偏差。即：“預測平均值”應當約等于“觀察平均值”

預測偏差指的是這兩個平均值之間的差值。即：預測偏差 = 預測平均值 - 數據集中相應標簽的平均值

如果出現非常高的非零預測偏差，則說明模型某處存在錯誤，因為這表明模型對正類別標簽的出現頻率預測有誤。

造成預測偏差的可能原因包括：

• 特征集不完整
• 數據集混亂
• 模型實現流水線中有錯誤？
• 訓練樣本有偏差
• 正則化過強

分桶偏差

邏輯回歸可預測 0 到 1 之間的值。不過，所有帶標簽樣本都正好是 0或 1。因此，在檢查預測偏差時，您無法僅根據一個樣本準確地確定預測偏差；您必須在“一大桶”樣本中檢查預測偏差。也就是說，只有將足夠的樣本組合在一起以便能夠比較預測值與觀察值，邏輯回歸的預測偏差才有意義。

稀疏性正則化

L1正則化

在高維度稀疏矢量中，最好盡可能使權重正好降至 0。正好為 0 的權重基本上會使相應特征從模型中移除。 將特征設為 0 可節省 RAM 空間，且可以減少模型中的噪點。

L2 正則化可以使權重變小，但是并不能使它們正好為 0.0。

L1 正則化這種正則化項的作用類似 L0，但它具有凸優化的優勢，可有效進行計算。因此，我們可以使用 L1 正則化使模型中很多信息缺乏的系數(權重)正好為 0，從而在推理時節省 RAM。

L1 和 L2 正則化。

L2 和 L1 采用不同的方式降低權重：

• L2 會降低權重2。
• L1 會降低 |權重|。

因此，L2 和 L1 具有不同的導數：

• L2 的導數為 2 * 權重。
• L1 的導數為 k（一個常數，其值與權重無關）。

神經網絡

神經網絡是更復雜版本的特征組合。實質上，神經網絡會學習適合您的相應特征組合。

**函數

要對非線性問題進行建模，我們可以直接引入非線性函數。我們可以用非線性函數將每個隱藏層節點像管道一樣連接起來。

常見**函數

S 型**函數將加權和轉換為介于 0 和 1 之間的值。
$F(x)=1 / (1+e^?x)$F(x)=1/(1+e?x)
相較于 S 型函數等平滑函數，以下修正線性單元**函數（簡稱為 ReLU）的效果通常要好一點，同時還非常易于計算。
$F(x)=max(0,x)$F(x)=max(0,x)
ReLU 的優勢在于它基于實證發現（可能由 ReLU 驅動），擁有更實用的響應范圍。S 型函數的響應性在兩端相對較快地減少。

系數(權重)正好為 0**，從而在推理時節省 RAM。

L1 和 L2 正則化。

L2 和 L1 采用不同的方式降低權重：

• L2 會降低權重2。
• L1 會降低 |權重|。

因此，L2 和 L1 具有不同的導數：

• L2 的導數為 2 * 權重。
• L1 的導數為 k（一個常數，其值與權重無關）。

神經網絡

神經網絡是更復雜版本的特征組合。實質上，神經網絡會學習適合您的相應特征組合。

**函數

要對非線性問題進行建模，我們可以直接引入非線性函數。我們可以用非線性函數將每個隱藏層節點像管道一樣連接起來。

常見**函數

S 型**函數將加權和轉換為介于 0 和 1 之間的值。
$F(x)=1 / (1+e^?x)$F(x)=1/(1+e?x)
相較于 S 型函數等平滑函數，以下修正線性單元**函數（簡稱為 ReLU）的效果通常要好一點，同時還非常易于計算。
$F(x)=max(0,x)$F(x)=max(0,x)
ReLU 的優勢在于它基于實證發現（可能由 ReLU 驅動），擁有更實用的響應范圍。S 型函數的響應性在兩端相對較快地減少。