leetcode第188題,買賣股票4,思路非常清晰
標簽: leecode
leetcode第188題,買賣股票4
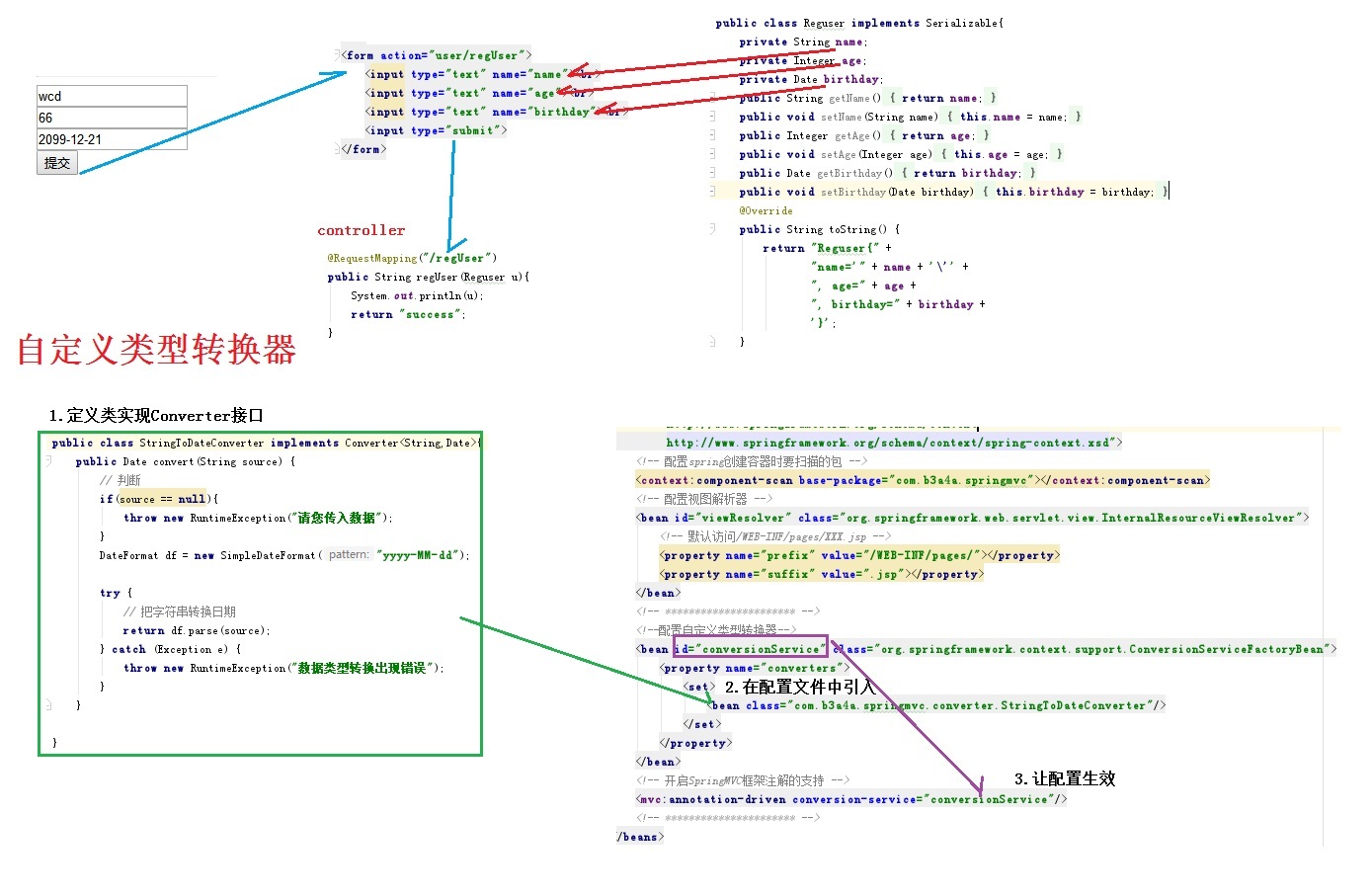
DP思考過程:首先總結出有哪些狀態,例如這題中,k代表交易次數,所有prices數組中每個元素都會有2k個狀態(即(買+賣)k=2k),所以此時我們可以創建一個2k長度的數組作為記錄,接下來分析狀態轉移
可以輕易想到buy=上一次sell的錢-prices[i];//這里注意第一次交易時sell=0;
sell=上一次buy的錢+prices[i];
這里leetcode有個坑,內存溢出問題,當2k很大時,這時的數組會非常大,導致內存溢出,優化方式:當2*k>=prices.length時,其實這時就是買賣股票2的情況,即無限次交易
好了,分析完了,接下來代碼過程
看不懂的可以留言或者私聊我
class Solution {
public int maxProfit(int k, int[] prices) {
int n = prices.length;
if(prices==null||prices.length<2||k<1)return 0;
//當2*k>=prices.length時,優化為maxPRofit2方法
if(2*k>=n)return maxProfit2(prices,n);
return maxProfit1(k,prices,n);
}
public int maxProfit1(int k,int[] prices,int n){
int[] memo = new int[2 * k];
for (int i = 0; i < k; i++) {
memo[2 * i] = Integer.MIN_VALUE;
}
for (int i = 0; i < n; i++) {
//記錄每個memo中的值以便 i++后使用
for (int j = 0; j < 2 * k; j++) {
if ((j & 1) == 0)//偶數為buy
memo[j] = Math.max(memo[j], j == 0? -prices[i] : memo[j - 1] - prices[i]);
else //奇數為sell
memo[j] = Math.max(memo[j], memo[j - 1] + prices[i]);
}
}
return memo[2 * k - 1];
}
private int maxProfit2(int[] prices,int n) {
int buy[]=new int[n];
int sell[]=new int[n];
buy[0]=-prices[0];
sell[0]=0;
for(int i=1;i<n;i++){
buy[i]=Math.max(buy[i-1], sell[i-1]-prices[i]);
sell[i]=Math.max(sell[i-1], buy[i-1]+prices[i]);
}
return sell[n-1];
}
}

智能推薦
requests實現全自動PPT模板
http://www.1ppt.com/moban/ 可以免費的下載PPT模板,當然如果要人工一個個下,還是挺麻煩的,我們可以利用requests輕松下載 訪問這個主頁,我們可以看到下面的樣式 點每一個PPT模板的圖片,我們可以進入到詳細的信息頁面,翻到下面,我們可以看到對應的下載地址 點擊這個下載的按鈕,我們便可以下載對應的PPT壓縮包 那我們就開始做吧 首先,查看網頁的源代碼,我們可以看到每一...
Linux C系統編程-線程互斥鎖(四)
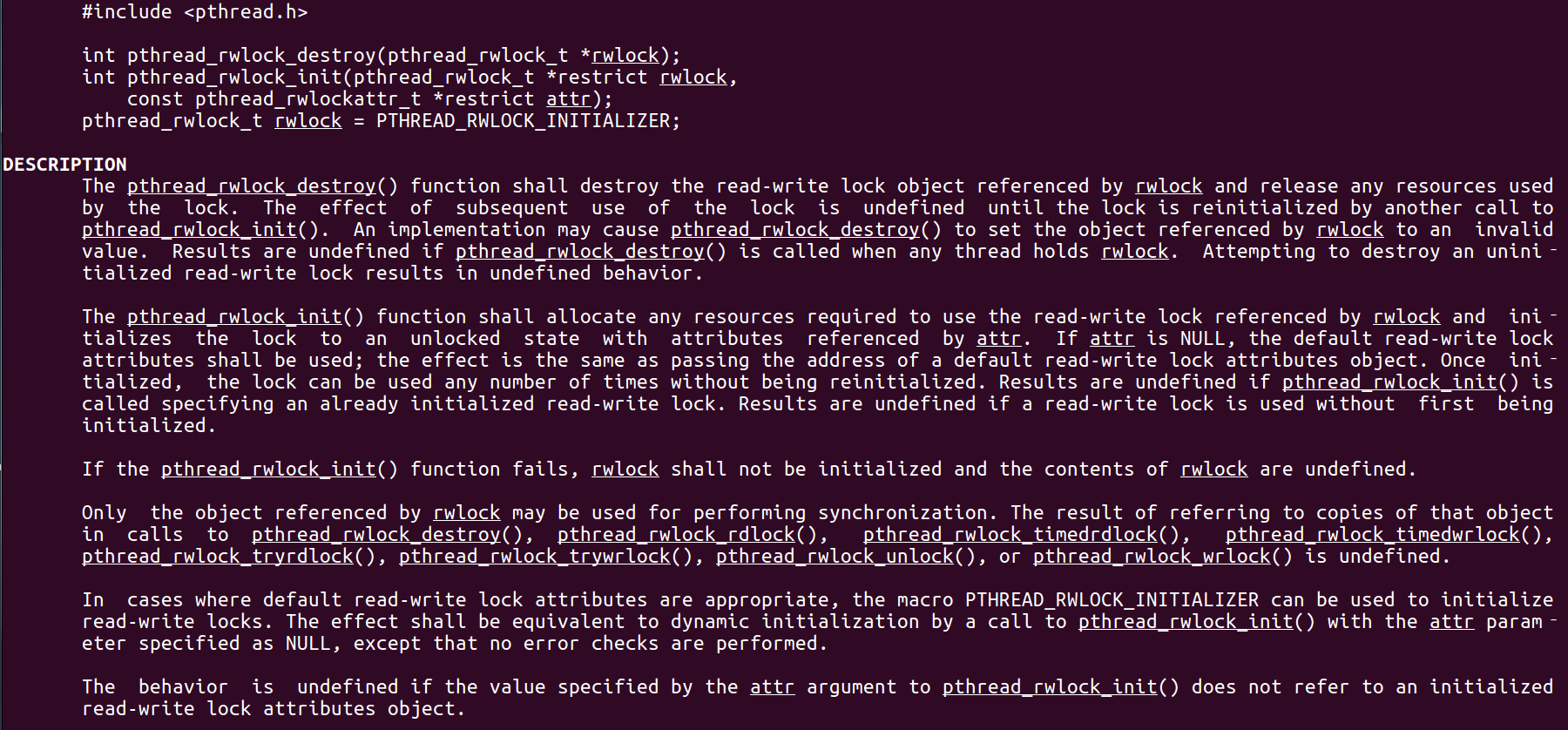
互斥鎖 互斥鎖也是屬于線程之間處理同步互斥方式,有上鎖/解鎖兩種狀態。 互斥鎖函數接口 1)初始化互斥鎖 pthread_mutex_init() man 3 pthread_mutex_init (找不到的情況下首先 sudo apt-get install glibc-doc sudo apt-get install manpages-posix-dev) 動態初始化 int pthread_...
統計學習方法 - 樸素貝葉斯
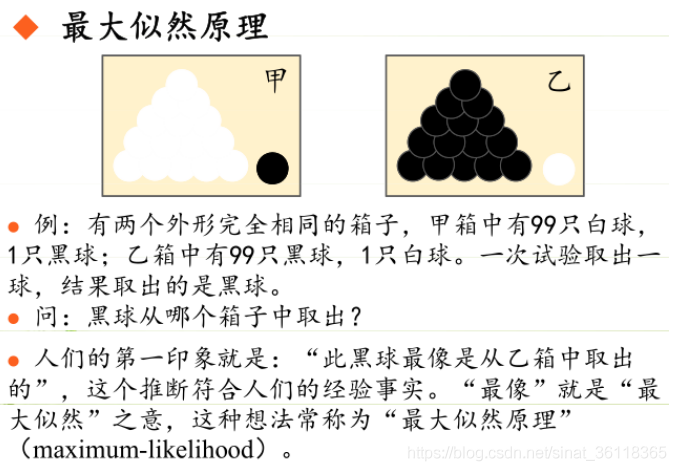
引入問題:一機器在良好狀態生產合格產品幾率是 90%,在故障狀態生產合格產品幾率是 30%,機器良好的概率是 75%。若一日第一件產品是合格品,那么此日機器良好的概率是多少。 貝葉斯模型 生成模型與判別模型 判別模型,即要判斷這個東西到底是哪一類,也就是要求y,那就用給定的x去預測。 生成模型,是要生成一個模型,那就是誰根據什么生成了模型,誰就是類別y,根據的內容就是x 以上述例子,判斷一個生產出...
styled-components —— React 中的 CSS 最佳實踐
https://zhuanlan.zhihu.com/p/29344146 Styled-components 是目前 React 樣式方案中最受關注的一種,它既具備了 css-in-js 的模塊化與參數化優點,又完全使用CSS的書寫習慣,不會引起額外的學習成本。本文是 styled-components 作者之一 Max Stoiber 所寫,首先總結了前端組件化樣式中的最佳實踐原則,然后在此基...
猜你喜歡
19.vue中封裝echarts組件
19.vue中封裝echarts組件 1.效果圖 2.echarts組件 3.使用組件 按照組件格式整理好數據格式 傳入組件 home.vue 4.接口返回數據格式...
【一只蒟蒻的刷題歷程】【藍橋杯】歷屆試題 九宮重排 (八數碼問題:BFS+集合set)
資源限制 時間限制:1.0s 內存限制:256.0MB 問題描述 如下面第一個圖的九宮格中,放著 1~8 的數字卡片,還有一個格子空著。與空格子相鄰的格子中的卡片可以移動到空格中。經過若干次移動,可以形成第二個圖所示的局面。 我們把第一個圖的局面記為:12345678. 把第二個圖的局面記為:123.46758 顯然是按從上到下,從左到右的順序記錄數字,空格記為句點。 本題目的任務是已知九宮的初態...
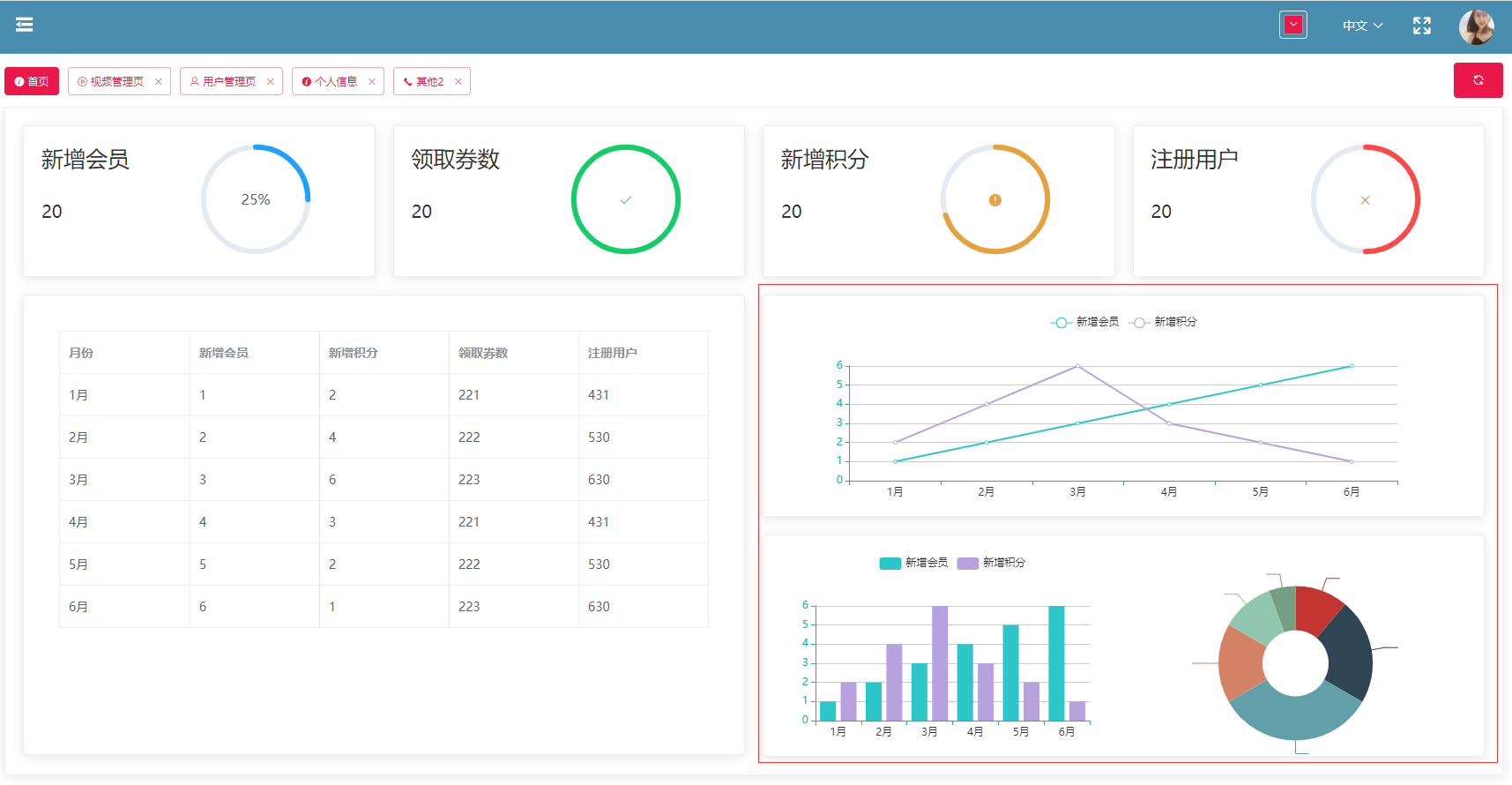
dataV組件容器寬高發生變化后,組件不會自適應解決方法
項目中需要大屏幕數據展示,于是使用了dataV組件,但是使用是發現拖動瀏覽器邊框,dataV組件顯示異常,如圖: 于是查了官網,官網的解釋如下: 于是按照官網的意思編寫代碼: 于是可以自適應了...