Codeforces Edu 87

C. Simple Polygon Embedding【三分+計算幾何】

題目

對于一個邊長為1的正$2n$2n邊形，求其最小覆蓋正方形的邊長

題解

如果$n$n為偶數，那么該正多邊形可以旋轉成如下形式

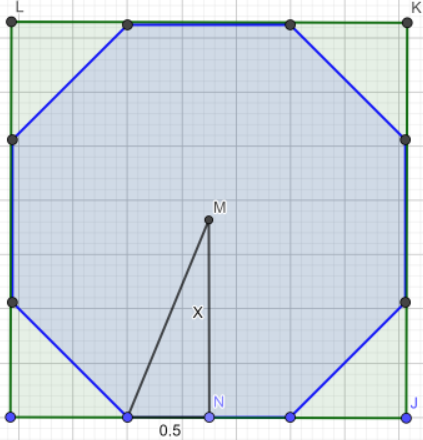
其中四條邊與正方形邊界平行，因此正方形的邊長計算公式為
$ans=\frac{1}{tan\frac{\pi}{2n}}$ans=tan2nπ?1?
而如果$n$n為奇數，不論怎么旋轉最多只有兩條邊與正方形邊界平行

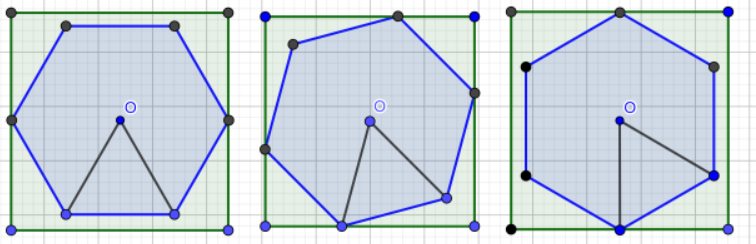
因此，可以用三分的方法在旋轉過程中找到一個最小覆蓋正方形。根據對稱性，旋轉角度只需要在$0\sim \frac{\pi}{2n}$0～2nπ?。實際上，由對稱性不難猜出，應該在旋轉的中間位置，即$\frac{\pi}{4n}$4nπ?取到最小值，因此公式為
$ans=\frac{\cos(\frac{\pi}{4n})}{\sin(\frac{\pi}{2n})}$ans=sin(2nπ?)cos(4nπ?)?
這里給出$n$n為奇數時用三分的方法尋找最小值的過程

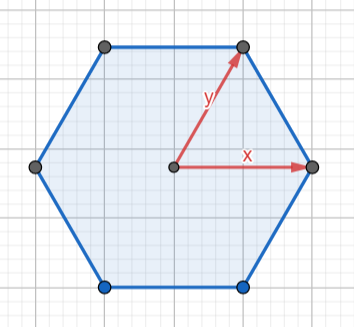
用兩個向量X,Y追蹤旋轉過程中最小覆蓋正方形邊長的變化，正方形的邊長就等于$max(X向量在x軸方向投影,Y向量在y軸方向投影)*2$max(X向量在x軸方向投影,Y向量在y軸方向投影)?2

題解

#include <bits/stdc++.h>
using namespace std;
#define mem(a,b) memset(a,b,sizeof(a))
#define endl '\n'
#define pi acos(-1)
typedef long long ll;
const int INF = 1 << 30;
const double eps = 1e-8;
struct Point {	// 點類
	double x, y;
	Point() {};
	Point(double x, double y): x(x), y(y) {}
	void operator=(const Point&a) {
		x = a.x, y = a.y;
	}
};
typedef Point Vector;
double Dot(Vector A, Vector B) {return A.x * B.x + A.y * B.y;}
double Cross(Vector A, Vector B) {return A.x * B.y - A.y * B.x;}
double Len(Vector A) {return sqrt(Dot(A, A));}	// 向量長度
Vector Rotate(Vector A, double rad)
// 向量逆時針旋轉
{
	return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));
}

int n;
Vector X, Y; // 分別監測旋轉過程中x,y的最小最大值

double cal(double rad)
// 計算旋轉后最小正方形邊長
{
	Vector tempx = Rotate(X, rad);
	Vector tempy = Rotate(Y, rad);
	return max(tempx.x, tempy.y) * 2;
}
double tsearch(double left, double right)
{
	double ans = INF;
	double mid, midmid;
	while (right - left > eps) {
		mid = (left + right) / 2;
		midmid = (mid + right) / 2;
		double ans1 = cal(mid), ans2 = cal(midmid);
		if (ans1 < ans2) {
			right = midmid;
			ans = min(ans, ans1);
		}
		else {
			left = mid;
			ans = min(ans, ans2);
		}
	}
	return ans;
}
int main()
{
	ios::sync_with_stdio(0), cin.tie(0);
	int t; cin >> t;
	while (t--) {
		cin >> n;
		X.x = 0.5 / sin(pi / (2 * n)), X.y = 0;
		Y.x = 0.5, Y.y = 0.5 / tan(pi / (2 * n));
		double sta = 0, end = pi / (2 * n);	// 旋轉范圍
		cout << fixed << setprecision(8) << tsearch(sta, end) << endl;
	}
	return 0;
}

D. Multiset【二分答案】

題目

給定一個具有$n$n個元素的集合，有$q$q次操作，每次操作給定一個整數$k$k，規則如下：

1. 如果$k\ge 1$k≥1，則把$k$k加入集合中；
2. 如果$k<0$k<0，則從集合中按升序排序后，移除第$|k|$∣k∣個元素

如果最終集合非空，輸出任一集合中元素即可

• Memory limit: 28mb

題解

本題可以選擇用線段樹之類的數據結構來模擬題目中的操作，但需要進行一定的優化，因為本題空間限制非常嚴格。

實際上，考慮到最終只需要輸出集合中的任意一個元素即可，不妨假設要輸出最小的一個，那么可以用二分答案的方法來查找。

二分查找的思路為：
定義函數count(x)表示：對于元素x，最終集合中小于等于x的元素個數。
最終答案就應該是找到一個最小的x滿足$count(x)>0$count(x)>0

因為在本題中，集合中元素不唯一，并且不一定是連續的。
假設最終集合中最小的元素是y，那么在二分過程中，任何大于等于y的數返回結果都是$\ge 1$≥1，而比y小的數返回結果都是0，因此y就是那個滿足count(x)>0的最小元素

對于最終集合為空的情況，可以用一個非常大的數去檢驗。因為集合中元素$a[i]\le 10^6$a[i]≤106，如果最終集合中小于等于$10^9$109的元素為0，就說明集合中不可能存在任何元素。（如果$count(1e9)==0$count(1e9)==0，就說明最終集合中的最小元素必定是大于$1e9$1e9的，而這與集合中元素$\le 1e6$≤1e6相矛盾）

if (count(int(1e9)) == 0) {
    cout << 0 << endl;
}

代碼

#include <bits/stdc++.h>
using namespace std;
#define mem(a,b) memset(a,b,sizeof(a))
#define endl '\n'
typedef long long ll;
const int maxn = 1e6 + 10;
int n, q;
vector<int>a, k;
int count(int x)
// 計算最終集合里面小于等于x的元素個數
{
	int cnt = 0;
	for (int i = 0; i < n; i++) {	// 初始化
		if (a[i] <= x) cnt++;
	}
	for (int i = 0; i < q; i++) {
		if (k[i] > 0 && k[i] <= x) cnt++;	// 插入正數，并且比x小，必然會排在x前面
		if (k[i] < 0 && abs(k[i]) <= cnt) cnt--;	// 插入負數，如果其絕對值<=cnt，就會刪除x左側的元素
	}
	return cnt;
}
int main()
{
	ios::sync_with_stdio(0), cin.tie(0);
	cin >> n >> q;
	a.resize(n); k.resize(q);
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	for (int i = 0; i < q; i++) {
		cin >> k[i];
	}
	if (count(int(1e9)) == 0) {	// 判斷最終集合是否為空
		cout << 0 << endl;
		return 0;
	}
	int left = 1, right = int(1e6) + 1;
	while (left < right) {
		int mid = left + (right - left) / 2;
		if (count(mid) <= 0) left = mid + 1;
		else right = mid;
	}
	cout << right << endl;
    return 0;
}