DC學院學習筆記(十六):線性回歸實戰
預測型數據分析:線性回歸
回歸:預測數值型變量
分類:預測樣本所屬類別
聚類:在未知樣本類別的情況下,根據樣本之間的相似性把樣本分成不同的類別
適用:用于股價、房價、空氣質量等數值型變量的預測
數學模型:分析兩組變量之間的關系
x:自變量(Independent variable)
y:應變量(Dependent variable)
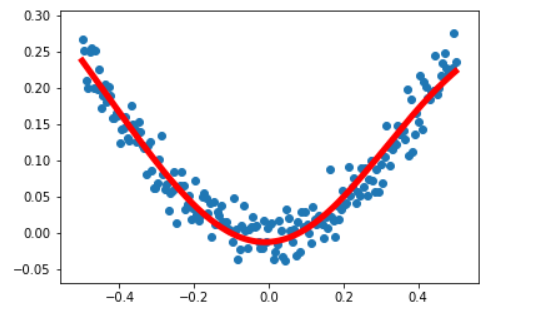
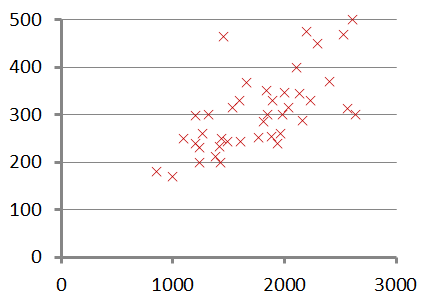
如圖是一個線性回歸的示意圖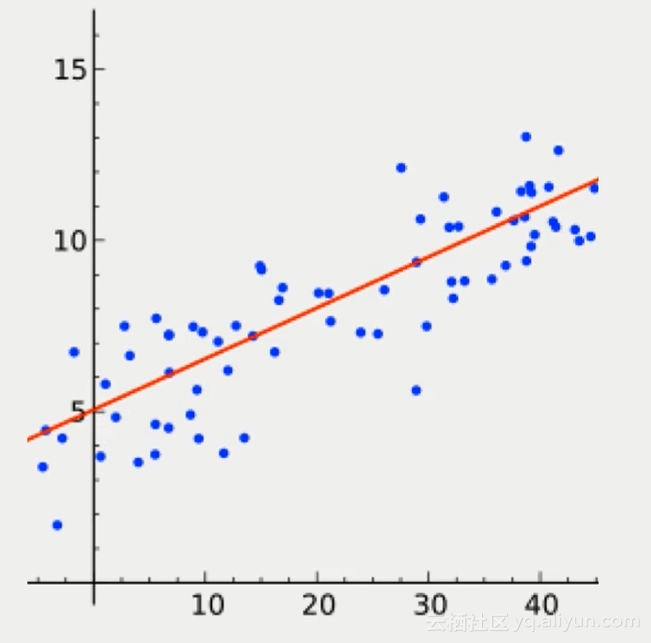
通過x來預測y,函數:f(x) = y,例如在房價問題中,用房子大小等特征作為自變量,房子價格為應變量
房價回歸預測案例:
$x_1$:房子大小
$x_2$:房子樓層
$x_3$:綠化規模
$x_4$:距離最近的地鐵站距離
$x_5$:距離最近的公交站距離
$x_6$:是否配備停車位
……
y:房子價格
根據常識來講,房價和很多因素相關,房子的大小、樓層等等都是比較明顯的影響因素,還有一些需要花功夫去尋找的特征。
要尋找一個函數f,將x映射到y上,這就是回歸的關鍵。
回歸的經典方法:線性回歸
線性回歸認為y是x的一個線性的疊加
-
方程式:
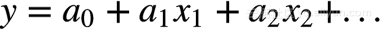
向量形式: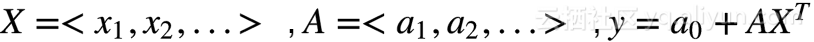
-
參數含義
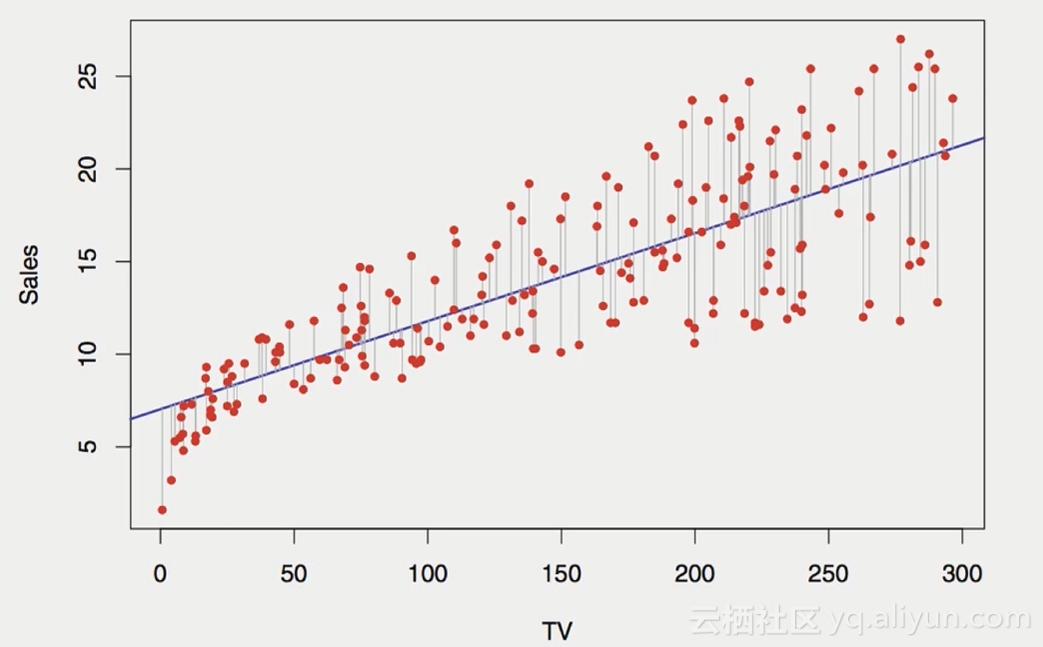
圖中y軸上的截距為,回歸曲線的斜率代表橫坐標變量的系數,即
-
參數優化方法:監督學習、OLS
- 監督學習:已有一些訓練樣本(訓練集),同時知道X和y,通過這些已知的樣本學習得到回歸模型
- OLS(Ordinary Least Squares):使得預測的y和真實的y在訓練集上誤差的平方最小
用sklearn實現
1.依舊使用到iris的數據集
import pandas
iris = pandas.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',header=None)
iris.columns=['SepalLengthCm','SepalWidthCm','PetalLengthCm','PetalWidthCm','Species']
iris.sample(10)
| SepalLengthCm | SepalWidthCm | PetalLengthCm | PetalWidthCm | Species | |
|---|---|---|---|---|---|
| 25 | 5.0 | 3.0 | 1.6 | 0.2 | Iris-setosa |
| 28 | 5.2 | 3.4 | 1.4 | 0.2 | Iris-setosa |
| 137 | 6.4 | 3.1 | 5.5 | 1.8 | Iris-virginica |
| 87 | 6.3 | 2.3 | 4.4 | 1.3 | Iris-versicolor |
| 126 | 6.2 | 2.8 | 4.8 | 1.8 | Iris-virginica |
| 30 | 4.8 | 3.1 | 1.6 | 0.2 | Iris-setosa |
| 86 | 6.7 | 3.1 | 4.7 | 1.5 | Iris-versicolor |
| 96 | 5.7 | 2.9 | 4.2 | 1.3 | Iris-versicolor |
| 84 | 5.4 | 3.0 | 4.5 | 1.5 | Iris-versicolor |
| 94 | 5.6 | 2.7 | 4.2 | 1.3 | Iris-versicolor |
2. 繪圖
import seaborn
%matplotlib inline
#通過畫圖可以直觀地對數據的線性關系做一個觀察
seaborn.regplot(x='PetalLengthCm',y='PetalWidthCm',data=iris)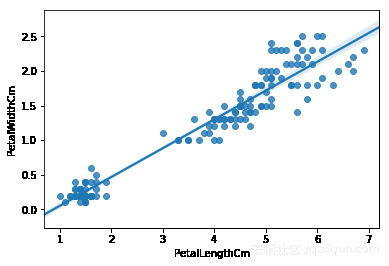
3.訓練模型
from sklearn import linear_model
lm=linear_model.LinearRegression()
features=['PetalLengthCm']
X=iris[features]
y=iris['PetalWidthCm']
print(X.shape,y.shape)(150, 1) (150,)
#放入兩個特征,X就會多一個維度
features=['PetalLengthCm','SepalLengthCm']
#使用X,y來訓練model
model=lm.fit(X,y)
print(model.intercept_,model.coef_)
#從print的結果可以得到回歸模型的截距和系數-0.366514045217 [ 0.41641913]
截距和系數正對應上圖中的直線
4.預測數據
#使用model來對數據進行預測,輸入X自變量的值,輸出y的預測值
#注意多個自變量時的情況,比如:model.predict([1,2])
model.predict(4)array([ 1.29916248])
預測性能的評估
為了評估獲得模型的性能,需要對數據集進行劃分,劃分為訓練集和測試集,在訓練集上學習獲得模型,在測試集上評估誤差
交叉檢驗
將數據集中的樣本等分成多份,每次取其中的一份作為測試集,剩余的數據作為訓練集,使用測試集數據評估和檢驗從訓練集學習得到的模型,即進行交叉檢驗。相對于隨機劃分,一部分的訓練集永遠劃分在測試集中,交叉檢驗是將數據劃分成若干份,每次用不同的部分作為測試集,則每份都被當做測試集和訓練集使用過。
如下圖是將數據集劃分為五份的交叉檢驗
將數據集分為5份,分別進行5次回歸
回歸常用的打分函數
- $MAE=\sum \left | {y}'-y \right |/N$對應的scoring參數為’neg_mean_absolute_error’
- $MSE=\sum ({y}'-y)^{2}$對應的scoring參數為’neg_mean_squared_error’
得分越高,則代表模型的性能越好
scikit learn中進行交叉檢驗
from sklearn.model_selection import cross_val_score
#得到5次交叉檢驗的誤差,注意這里cross_val_score()前面用了負號,得到的是每個回歸模型的平均絕對值誤差
#用MAE舉例
scores=-cross_val_score(lm,X,y,cv=5,scoring='neg_mean_absolute_error')
print(scores)
#求平均值,作為誤差結果
import numpy as np
print(np.mean(scores))[ 0.08581817 0.09533821 0.13792154 0.2074044 0.29904645]
0.165105751004
智能推薦
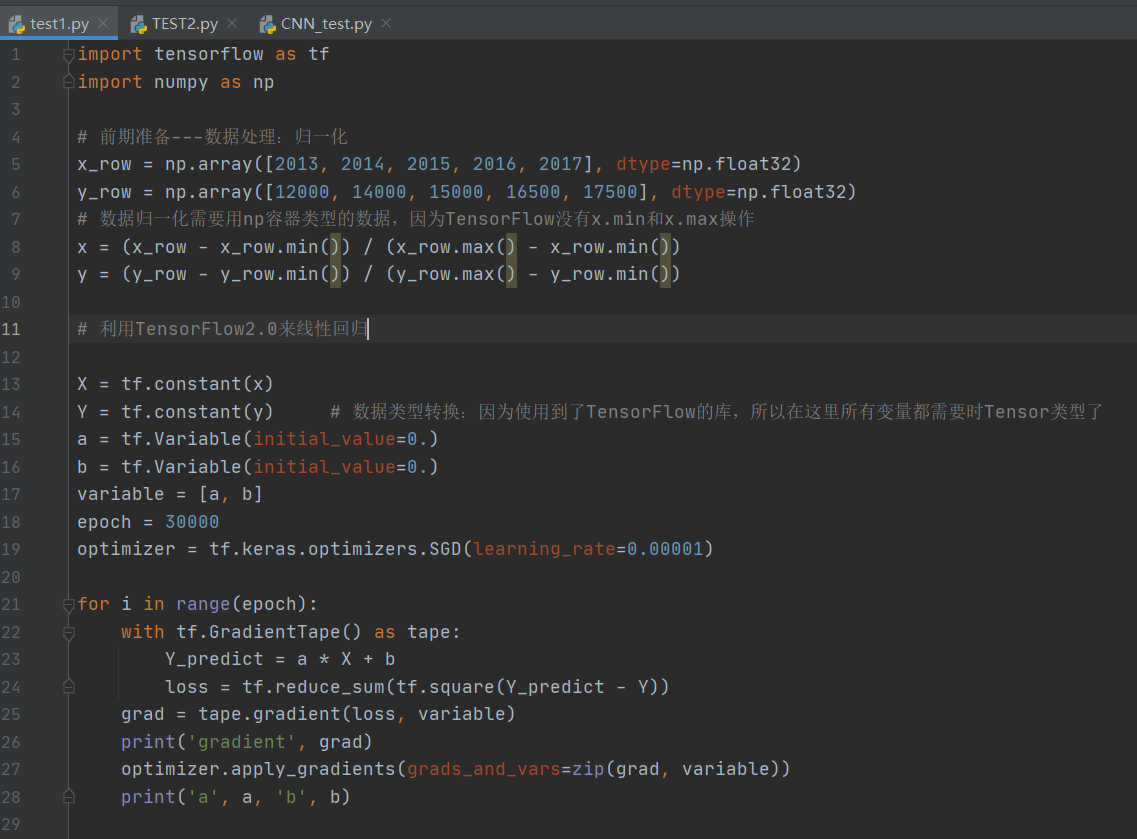
TensorFlow2.0學習筆記——簡單的線性回歸實戰
代碼: 代碼解析: 1.第15-16行 但是如果改成下面這樣,則會報錯: 因為tf.Variable默認整數為int32,注意Numpy默認的浮點數類型是float64,前面的x y定義為類型:dtype=np.float32 如果想和Numpy數據進行對比或者一起參與求導運算,則需要修改與numpy一致。 2.第19行 設置了優化器選用SGD優化器(SGD梯度下降算法),梯度下降的...
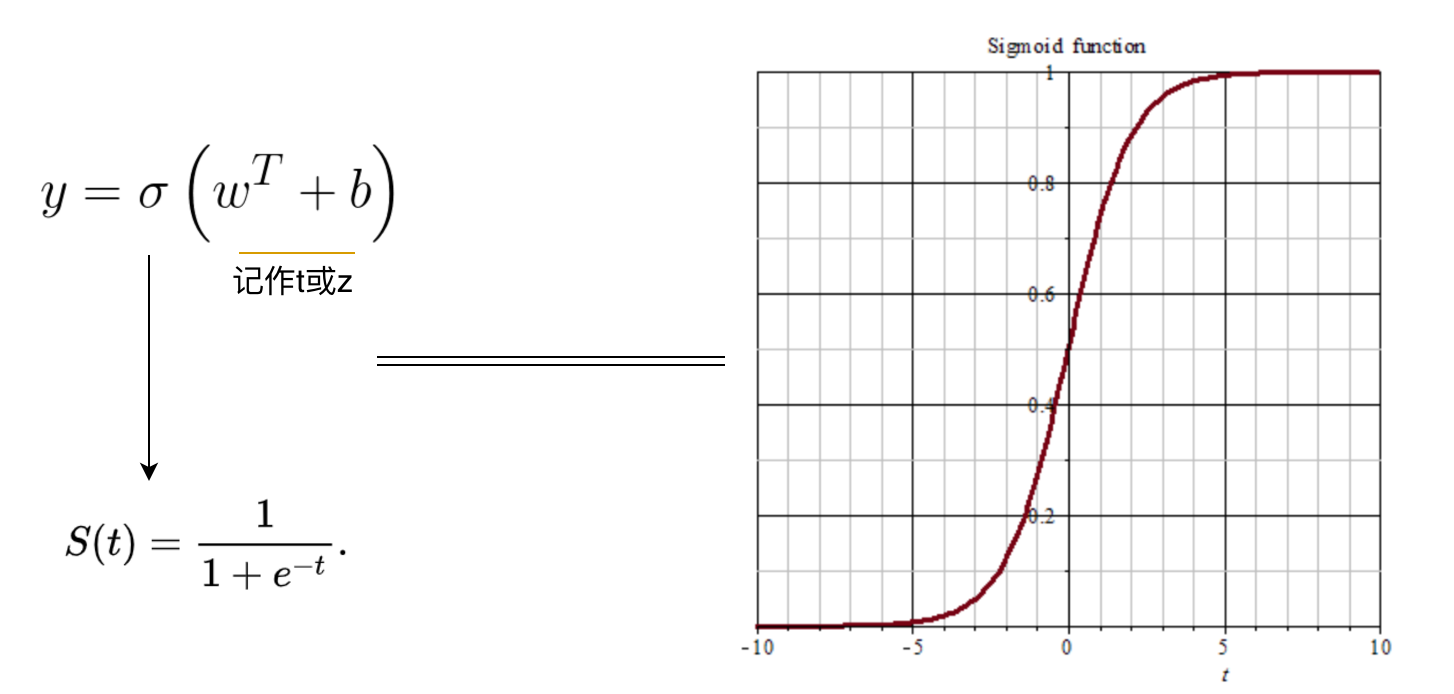
CNN學習筆記:線性回歸
CNN學習筆記:Logistic回歸 線性回歸 二分類問題 Logistic回歸是一個用于二分分類的算法,比如我們有一張圖片,判斷其是否為一張貓圖,為貓輸出1,否則輸出0。 基本術語 進行機器學習,首先要有數據,比如我們收集了一批關于西瓜的數據,例如 (色澤=青綠;根蒂=收縮;敲聲=濁響) (色澤=烏黑;根蒂=稍蜷;敲聲=沉悶) (色澤=淺白;根蒂=硬挺;敲聲=清脆) ...
機器學習筆記——線性回歸
機器學習筆記——線性回歸 學習資源:斯坦福機器學習公開課 by Andrew Ng 0 符號說明 mm:訓練樣本個數 nn:樣本的特征個數(特征的維度),這里先取n=1n=1 hθ(x)hθ(x):假設函數,hθ(x)=θ0+θ1xhθ(x)=θ0+θ1x J(θ0,...
猜你喜歡
freemarker + ItextRender 根據模板生成PDF文件
1. 制作模板 2. 獲取模板,并將所獲取的數據加載生成html文件 2. 生成PDF文件 其中由兩個地方需要注意,都是關于獲取文件路徑的問題,由于項目部署的時候是打包成jar包形式,所以在開發過程中時直接安照傳統的獲取方法沒有一點文件,但是當打包后部署,總是出錯。于是參考網上文章,先將文件讀出來到項目的臨時目錄下,然后再按正常方式加載該臨時文件; 還有一個問題至今沒有解決,就是關于生成PDF文件...
電腦空間不夠了?教你一個小秒招快速清理 Docker 占用的磁盤空間!
Docker 很占用空間,每當我們運行容器、拉取鏡像、部署應用、構建自己的鏡像時,我們的磁盤空間會被大量占用。 如果你也被這個問題所困擾,咱們就一起看一下 Docker 是如何使用磁盤空間的,以及如何回收。 docker 占用的空間可以通過下面的命令查看: TYPE 列出了docker 使用磁盤的 4 種類型: Images:所有鏡像占用的空間,包括拉取下來的鏡像,和本地構建的。 Con...
requests實現全自動PPT模板
http://www.1ppt.com/moban/ 可以免費的下載PPT模板,當然如果要人工一個個下,還是挺麻煩的,我們可以利用requests輕松下載 訪問這個主頁,我們可以看到下面的樣式 點每一個PPT模板的圖片,我們可以進入到詳細的信息頁面,翻到下面,我們可以看到對應的下載地址 點擊這個下載的按鈕,我們便可以下載對應的PPT壓縮包 那我們就開始做吧 首先,查看網頁的源代碼,我們可以看到每一...
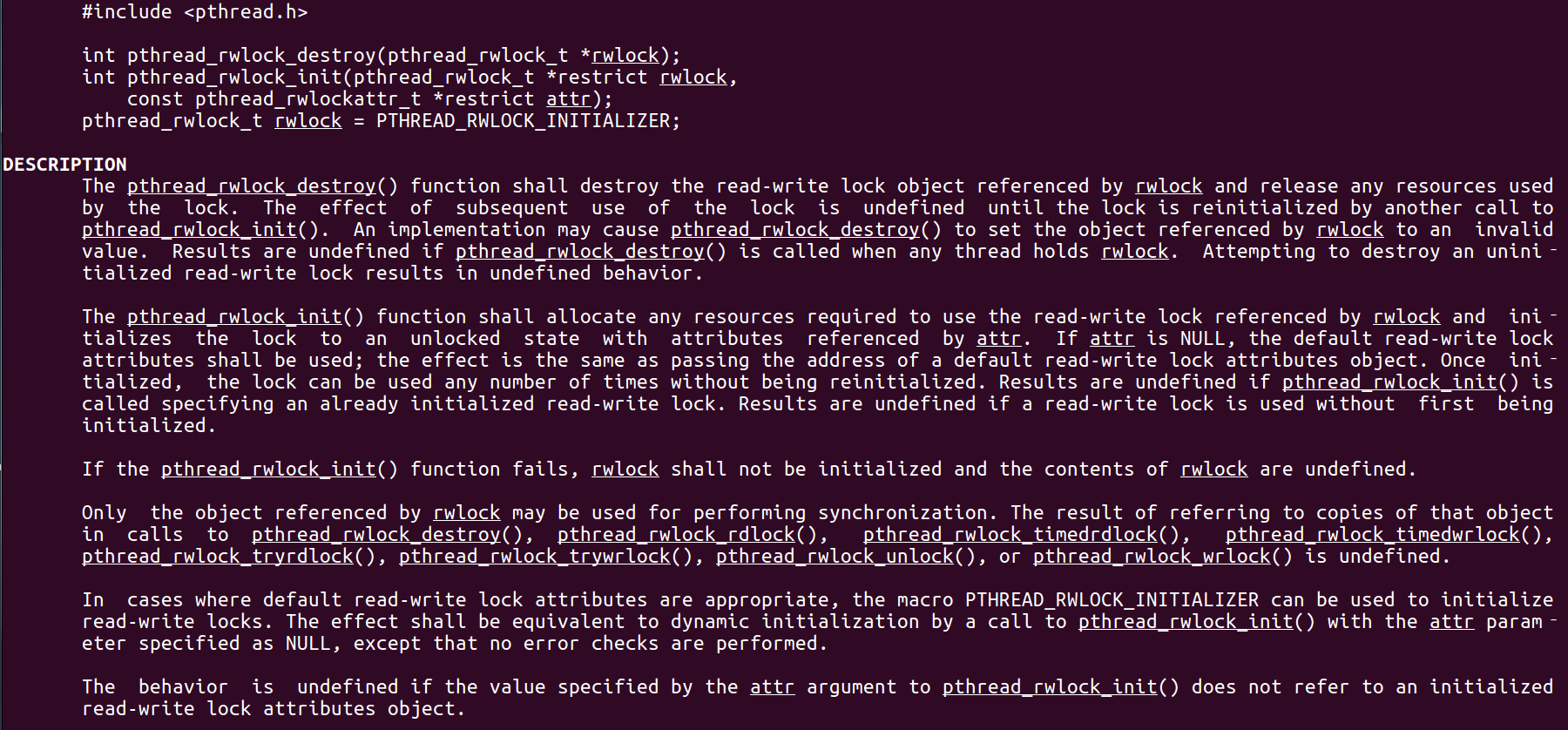
Linux C系統編程-線程互斥鎖(四)
互斥鎖 互斥鎖也是屬于線程之間處理同步互斥方式,有上鎖/解鎖兩種狀態。 互斥鎖函數接口 1)初始化互斥鎖 pthread_mutex_init() man 3 pthread_mutex_init (找不到的情況下首先 sudo apt-get install glibc-doc sudo apt-get install manpages-posix-dev) 動態初始化 int pthread_...