B-Tree和B+Tree學習筆記

標簽：學習筆記數據結構指針

B-Tree和B+Tree學習筆記

文章目錄

B-Tree和B+Tree學習筆記

1. B-Tree

1.1 定義

全稱Balance-tree(平衡多路查找樹)，平衡的意思是左邊和右邊分布均勻。多路的意思是相對于二叉樹而言的，二叉樹是二路查找樹，而B-tree有多條路。

B-Tree的階指的是節點最大的孩子數目。

我的理解是在二叉樹的基礎上增加了規則：

若根節點非葉子節點，則其至少有兩棵子樹
除了根節點和葉子節點之外，每個節點有k-1個key和k個孩子，其中**m/2上取整-1 ≤ k ≤ m-1**
所有葉子節點在同一層次
key按序排列

1.2 圖例

如下圖是一個階m=3的B-Tree：

3階B樹

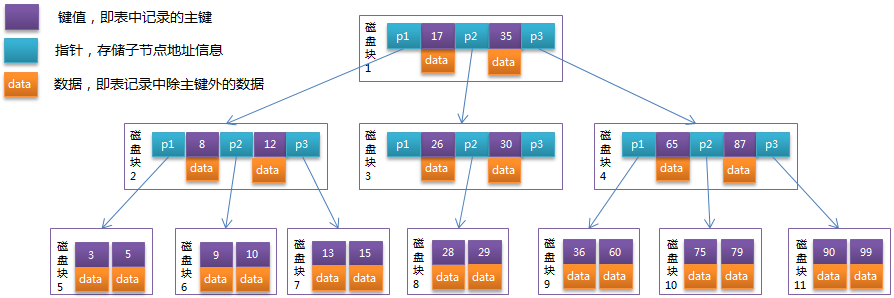
1.3 用途

顯著減少定位記錄時經歷的過程。一般用于數據庫的索引。

因為B樹相對AVL樹之類的結構而言具有一個節點存多個數據以及較為矮胖的特性，所以可以顯著降低訪問磁盤帶來的IO開銷。

~~對比B樹和平衡二叉樹，是否因為顯著減少層高，減少了磁盤IO？~~

1.4 代碼實現

1.4.1 數據結構定義

節點類型

所有非終端節點中包含(n,A0,K1,A1,K2,A2…,Kn,An)。

其中n為關鍵字個數，Ki為關鍵字，Ai-1為小于Ki的節點指針，Ai為大于Ki的節點指針。

// 結點類型
typedef struct BTNode
{
    int keynum;                //結點關鍵字個數
    struct BTNode *parent;     //指向雙親結點
    KeyType key[m + 1];        //關鍵字數組，0號單元未用
    struct BTNode *ptr[m + 1]; //孩子結點指針數組
    Record recptr[m + 1];      //記錄數組，0號單元未用
    BTNode() : keynum(), parent(), key(), ptr(), recptr() {}
} BTNode, *BTree;

查找結果類型

用于記錄在B-Tree中的查找結果。

// 查找結果類型
struct Result
{
    BTNode *pt; //指向找到的結點
    int i;      //在結點中的關鍵字位置;
    bool found; //查找成功與否標志
    Result() : pt(), i(), found() {}
    Result(BTNode *pt, int i, bool found) : pt(pt), i(i), found(found) {}
};

1.4.2 實現查找

SearchBTNode()函數

在結點p中查找關鍵字k的位置 i

**i **使得：p->key[i] <= k < p->key[i+1]

找到對應key則 i 就是key的下標，沒找到對應key則 i 就是繼續向下查找的指針的下標
```
int SearchBTNode(BTNode *p, KeyType k)
{
    int i = 0;
    while (i < p->keynum && k >= p->key[i + 1])
        i++;
    return i;
}
```

SearchBTree()函數

在樹t上查找關鍵字k,返回結果(pt,i,tag)

成功則tag=1,關鍵字k是指針pt所指結點中第i個關鍵字

失敗則tag=0,關鍵字k的插入位置為pt結點的第i個

Result SearchBTree(BTree t, KeyType k)
{
    // 初始化，p指向待查節點，q指向p的雙親
    BTNode *p = t;
    BTNode *q = nullptr;
    bool found = false;
    int i = 0;
    //while循環查找過程，條件1：p非空（沒到葉子節點），條件2：還沒找到
    while (p && !found)
    {
        i = SearchBTNode(p, k);
        if (i > 0 && p->key[i] == k)
            found = true;
        else
        {
            q = p;
            p = p->ptr[i];
            found = false;
        }
    }
    if (found)
        return Result(p, i, 1); // 查找成功，返回其在B樹中位置
    else
        return Result(q, i, 0); // 查找不成功，返回其插入位置
}

1.4.3 實現插入

InsertBTNode()函數

將關鍵字k和結點q分別插入到p->key[i+1]和p->ptr[i+1]中

void InsertBTNode(BTNode *&p, int i, KeyType k, BTNode *q)
{
    // i+1之后（包括原i+1）整體后移，空出位置i+1
    int j;
    for (j = p->keynum; j > i; j--)
    {
        p->key[j + 1] = p->key[j];
        p->ptr[j + 1] = p->ptr[j];
    }
    // 插入k和q
    p->key[i + 1] = k;
    p->ptr[i + 1] = q;
    if (q != nullptr)
        q->parent = p;
    p->keynum++;
}

SplitBTNode()函數

將插入新節點后的節點p（含有m個key，已經節點過大）分裂成兩個結點，并返回分裂點x

KeyType SplitBTNode(BTNode *&p, BTNode *&q)
{
    int s = (m + 1) / 2;
    q = new BTNode;        //新建節點q
    q->ptr[0] = p->ptr[s]; //后一半移入節點q
    for (int i = s + 1; i <= m; i++)
    {
        q->key[i - s] = p->key[i];
        q->ptr[i - s] = p->ptr[i];
        q->recptr[i - s] = p->recptr[i];
    }
    q->keynum = p->keynum - s; //節點q存放m-s個
    q->parent = p->parent;
    //轉移到節點q之后，修改雙親指針
    for (int i = 0; i <= q->keynum; i++)
    {
        if (q->ptr[i] != nullptr)
            q->ptr[i]->parent = q;
    }
    p->keynum = s - 1; //節點p存放s個，但保留s-1個，p中最后一個key作為分裂點x
    return p->key[s];
}

NewRoot()函數

當【t為空樹】或【原根節點p分裂為p和q】時使用

生成新的根結點t，原結點p和結點q為子樹指針

void NewRoot(BTree &t, KeyType k, BTNode *p, BTNode *q)
{
    t = new BTNode;
    t->keynum = 1;
    t->ptr[0] = p;
    t->ptr[1] = q;
    t->key[1] = k;
    // 調整結點p和結點q的雙親指針
    if (p != nullptr)
        p->parent = t;
    if (q != nullptr)
        q->parent = t;
    t->parent = nullptr;
}

InsertBTree()函數

在樹t上結點p的key[i]之后插入關鍵字k

若引起結點過大，則嘗試向上分裂

Status InsertBTree(BTree &t, int i, KeyType k, BTNode *p)
{
    bool finished = false;
    BTNode *q = nullptr;
    KeyType x = k;
    while (p && !finished)
    {
        InsertBTNode(p, i, x, q);
        if (p->keynum < m)
            finished = true;
        else
        {
            x = SplitBTNode(p, q);
            //若p的雙親存在，在雙親節點中找x的插入位置
            p = p->parent;
            if (p)	i = SearchBTNode(p, x);
        }
    }
    //未完成，情況1：t是空樹（初始p為nullptr），情況2：根節點分裂為p和q
    if (!finished)
    {
        p = t; //原t即為p
        NewRoot(t, x, p, q);
    }
    return OK;
}

1.4.4 實現刪除

AdjustBTree()函數

刪除節點p中的第i個關鍵字后，調整B樹

在刪除操作后，如果非根節點出現節點關鍵字個數不足的情況，會使用AdjustBTree()函數來調整B樹。

假設刪除的key為k，它所在節點的雙親節點為p：
- k在p的最左孩子節點中：
  - 右兄弟夠借：p的最左key移入k所在節點，右兄弟的最左key移入p。
  - 右兄弟不夠借：將p中的Ki和右兄弟中的全部key一起合并到k所在節點。
- k在p的最右孩子節點中：
  - 左兄弟夠借：p的最右key移入k所在節點，左兄弟的最右key移入p。
  - 左兄弟不夠借：將p中的Ki和k所在節點剩余的key一起合并到左兄弟。
- k在p的中間孩子節點中：
  - 左兄弟夠借：p的最右key移入k所在節點，左兄弟的最右key移入p。
  - 右兄弟夠借：p的最左key移入k所在節點，右兄弟的最左key移入p。
  - 都不夠借：將p中的Ki和k所在節點剩余的key一起合并到左兄弟。
```
void AdjustBTree(BTNode *p, int i)
{
    // 刪除的是最左孩子節點中的關鍵字
    if (i == 0)
        if (p->ptr[1]->keynum > keyNumMin) //右節點夠借
            MoveLeft(p, 1);
        else //右節點不夠借
            Combine(p, 1);
    // 刪除的是最右孩子節點中的關鍵字
    else if (i == p->keynum)
        if (p->ptr[i - 1]->keynum > keyNumMin) //左節點夠借
            MoveRight(p, p->keynum);
        else //左節點不夠借
            Combine(p, p->keynum);
    // 刪除的是中間孩子節點中的關鍵字且左節點夠借
    else if (p->ptr[i - 1]->keynum > keyNumMin)
        MoveRight(p, i);
    // 刪除的是中間孩子節點中的關鍵字且右節點夠借
    else if (p->ptr[i + 1]->keynum > keyNumMin)
        MoveLeft(p, i + 1);
    // 刪除的是中間孩子節點中的關鍵字且左右都不夠借
    else
        Combine(p, i);
}
```

BTNodeDelete()函數

在節點p中查找并刪除關鍵字k，若未找到則遞歸向下刪除

bool BTNodeDelete(BTNode *p, KeyType k)
{
    int i;
    bool found; //查找標志
    if (p == nullptr)
        return 0;
    else
    {
        found = FindBTNode(p, k, i); //返回查找結果
        //查找成功
        if (found)
        {
            //刪除的是非葉子節點的關鍵字
            //理解i-1：若為非葉子節點，被刪除關鍵字為key[i]，則ptr[i-1]一定存在
            if (p->ptr[i - 1] != nullptr)
            {
                p->key[i] = FindReplace(p->ptr[i]); //尋找相鄰關鍵字(右子樹中最小的關鍵字)
                BTNodeDelete(p->ptr[i], p->key[i]); //執行刪除操作
            }
            else
                Remove(p, i); //從節點p中位置i處刪除關鍵字
        }
        else
            found = BTNodeDelete(p->ptr[i], k); //沿孩子節點遞歸查找并刪除關鍵字k
        // 非葉子節點刪除后可能從右子樹替補，可能會使右子樹關鍵字個數不足
        if (p->ptr[i] != nullptr)
            if (p->ptr[i]->keynum < keyNumMin) //刪除后關鍵字個數不足
                AdjustBTree(p, i);             //調整B樹
        return found;
    }
}

BTreeDelete()函數

刪除操作，在B樹中刪除關鍵字k

調用BTNodeDelete()函數

void BTreeDelete(BTree &t, KeyType k)
{
    bool deleted = BTNodeDelete(t, k); //刪除關鍵字k
    //查找失敗
    if (!deleted)
        printf("key[%d] is not exist!\n", k);
    //刪除后根節點無key
    else if (t->keynum == 0)
    {
        BTNode *p = t;
        t = t->ptr[0];
        delete p;
    }
}

DestroyBTree()函數

遞歸釋放B樹

void DestroyBTree(BTree &t)
{
    if (!t)
        return;
    BTNode *p = t;
    for (int i = 0; i <= p->keynum; i++)
        DestroyBTree(p->ptr[i]);
    delete p;
    t = nullptr;
}

1.4.5 實現層序遍歷

這部分主要使用隊列進行廣度優先搜索，完成層序遍歷，打印B樹

重點是使用length記錄每次的隊列長度，控制每輪循環打印的節點個數剛好等于這一層的節點數

LevelTraverse()函數

層序遍歷

void LevelTraverse(BTree t)
{
    queue<BTNode *> que;
    BTNode *p;
    int length;    //隊列長度，用于控制每一層的節點個數
    int level = 0; //記錄層數

    que.push(t);
    while (!que.empty())
    {
        length = que.size(); // 獲取當前隊列長度，用于分層
        //打印當前層所有節點
        printf("\tLevel %-2d:", level++);
        for (int i = 0; i < length; i++)
        {
            // 彈出頭節點作為當前節點
            p = que.front();
            que.pop();
            // 打印當前節點
            printf("[");
            printf("%d", p->key[1]);
            for (int j = 2; j <= p->keynum; j++)
            {
                printf(", %d", p->key[j]);
            }
            printf("]  ");
            // 把當前節點的所有非空子節點加入隊列
            for (int j = 0; j <= p->keynum; j++)
            {
                if (p->ptr[j] && p->ptr[j]->keynum != 0)
                    que.push(p->ptr[j]);
            }
        }
        printf("\n");
    }
}

PrintBTree()函數

打印B樹

Status PrintBTree(BTree t)
{
    if (t == NULL)
    {
        printf("\tEmpty B-Tree!\n");
        return EMPTY;
    }
    LevelTraverse(t);
    return OK;
}

1.4.6 測試

測試B樹各項功能

測試流程：

創建一棵m階（m=5）B樹，其中的key從1到16
打印菜單，可選操作有：
- Init 初始化B樹
- Insert 插入key
- Delete 刪除key
- Destroy 銷毀B樹
- Exit 退出程序
進行操作觀察輸出

如下圖是m=5，key從1到16的B樹：

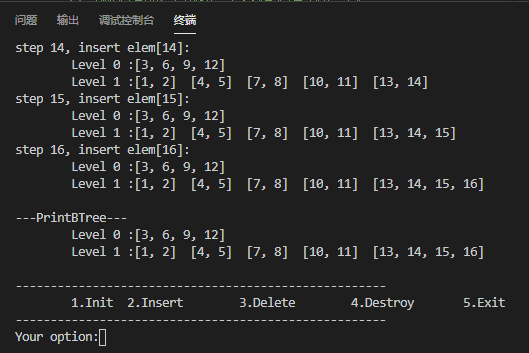
2. B+Tree

2.1 B-Tree的不足

遍歷時使用中序遍歷，往返于節點之間，增加磁盤塊讀寫開銷
非葉子節點同時存儲key和data，一個節點能存放的key數目受限，使樹長高
查詢性能不穩定
范圍查詢不友好

2.2 B+Tree的特點

葉子節點包含全部關鍵字
葉子節點之間用指針串接，遍歷時直接從葉子節點的頭指針開始
非葉子節點只存儲key，data全部存放在葉子節點
所有非葉子節點可以看作索引，只存放其孩子的最大（或最小）key
查詢性能穩定
范圍查詢友好

2.3 圖例

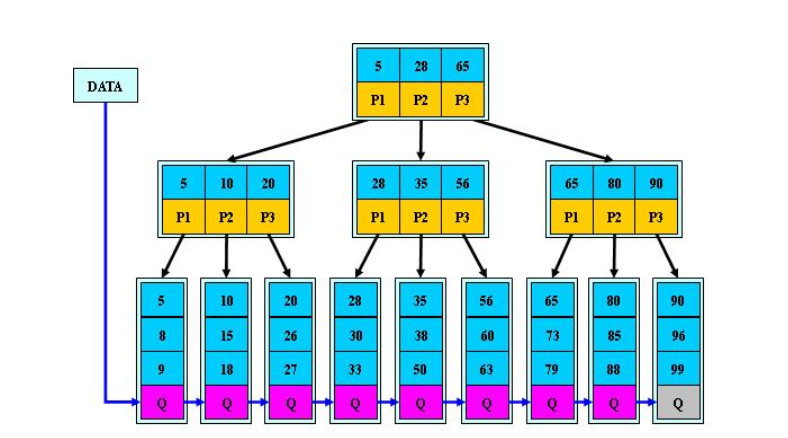
如下圖是一個階m=4的B+Tree：

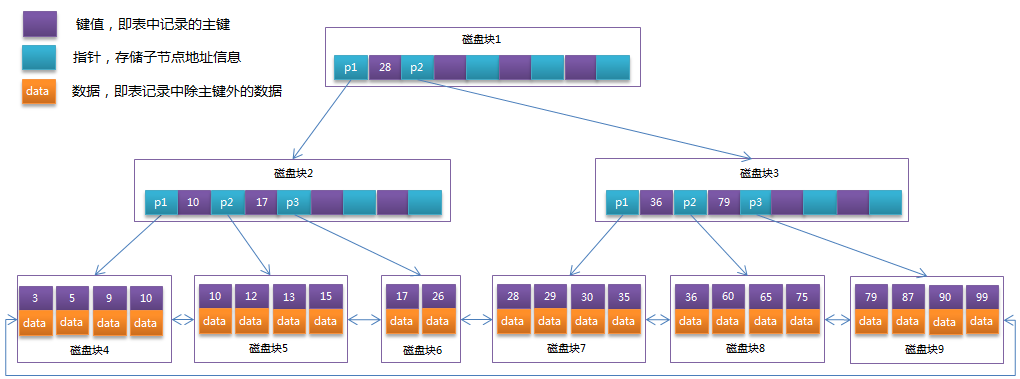
4階BPlus樹

圖中非葉子節點存放的是其孩子的最小key，圖左下的磁盤塊4有問題，key=10的索引不應該出現在這個磁盤塊里。

3. 對比B-Tree和B+Tree

3.1 差別

	B-Tree	B+Tree
n個關鍵字	n+1個分支	n個分支
節點內關鍵字個數	[m/2(上取整)-1,m-1]，根節點[1,m-1]	[m/2(上取整),m]，根節點[2,m]
葉子節點	關鍵字不全	包含全部關鍵字，指針指向記錄
非葉子節點	含data	不含data，只存索引
葉子節點鏈表	無	有

3.2 圖例

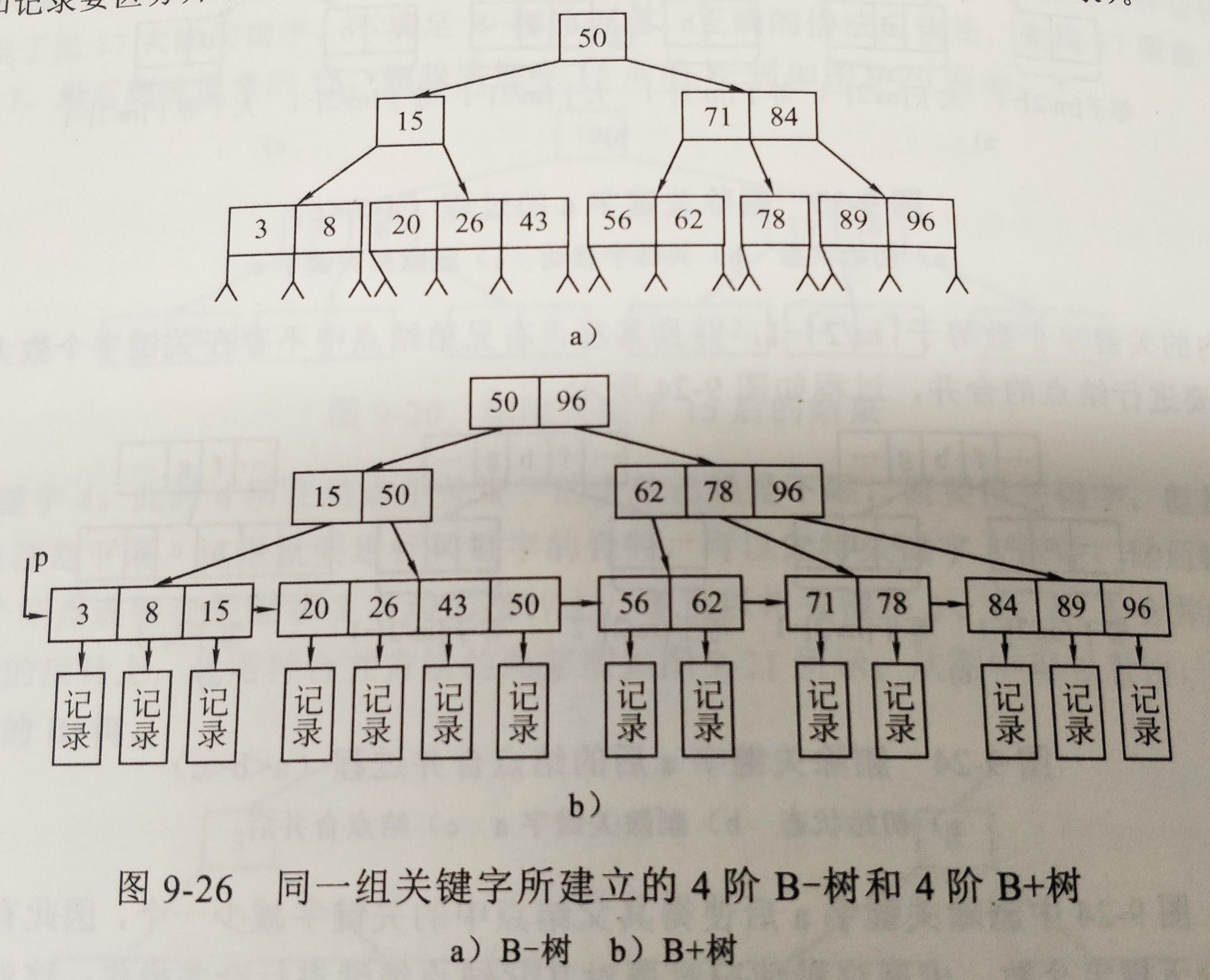
對比B和BPlus

本文鏈接：https://blog.csdn.net/weixin_42344299/article/details/109630922

智能推薦

紅黑樹—BTree

什么叫紅黑樹？同AVL樹一樣，紅黑樹也是近似平衡的二叉搜索樹，與AVL樹不同的是紅黑樹沒有了平衡因子，但增加了一個枚舉變量，來標明結點的顏（RED or BLACK）。因為紅黑樹可以保證它的最長路勁不超過它最短路徑的兩倍，所以它近似平衡。紅黑樹具有以下幾點性質： 1. 每個結點都必須具有一種顏色（RED or BLACK）。 2. 根結點為黑色。 3. 如果...

數據庫中的BTree和B+Tree

B+樹索引是B+樹在數據庫中的一種實現，是最常見也是數據庫中使用最為頻繁的一種索引。B+樹中的B代表平衡（balance），而不是二叉（binary），因為B+樹是從最早的平衡二叉樹演化而來的。在講B+樹之前必須先了解二叉查找樹、平衡二叉樹（AVLTree）和平衡多路查找樹（B-Tree），B+樹即由這些樹逐步優化而來。二叉...

PostgreSQL中BRIN和BTREE索引的比較（一） PostgreSQL 9.5引入了Block Range Index，簡稱BRIN，用于字段值和在表中的物理位置具有一定關聯關系的大數據量訪問。但是BRIN對于不同數據分布帶來的性能提升有多少，和傳統的BTREE索引比較性能又有什么差別，恐怕大家還沒有一個直觀的印象。本文將就這些問題嘗試給出一些解答，希望可以幫助大家在選擇BTREE或者B...

PostgreSQL DBA(47) - Index(Btree)

本節簡單介紹了PostgreSQL中的Btree索引,包括Btree的基本結構/NULL值處理/自定義類型支持等相關信息. 結構 Btree是常見的數據結構,有以下特性: 1.Btree是平衡樹,以root節點為分界,左右兩邊的中間節點數目一樣,也就是說查詢任意一個值,時間都是一樣的 2.Btree有多個分支,每個page(8KB)可以有數百個TIDs,也就是說Btree只需要不多的幾個層次就可以...

Btree與b+tree

1. Btree： B-tree是一種多路自平衡搜索樹，它類似普通的二叉樹，但是Btree允許每個節點有更多的子節點。Btree示意圖如下： B樹的搜索，從根結點開始，如果查詢的關鍵字與結點的關鍵字相等，那么就命中；否則，如果查詢關鍵字比結點關鍵字小，就進入左兒子；如果比結點關鍵字大，就進入右兒子；如果左兒子或右兒子的指針為空，則報告找不到相應的關鍵字；如果B樹的所有非葉子結點的左右子樹的結點數...