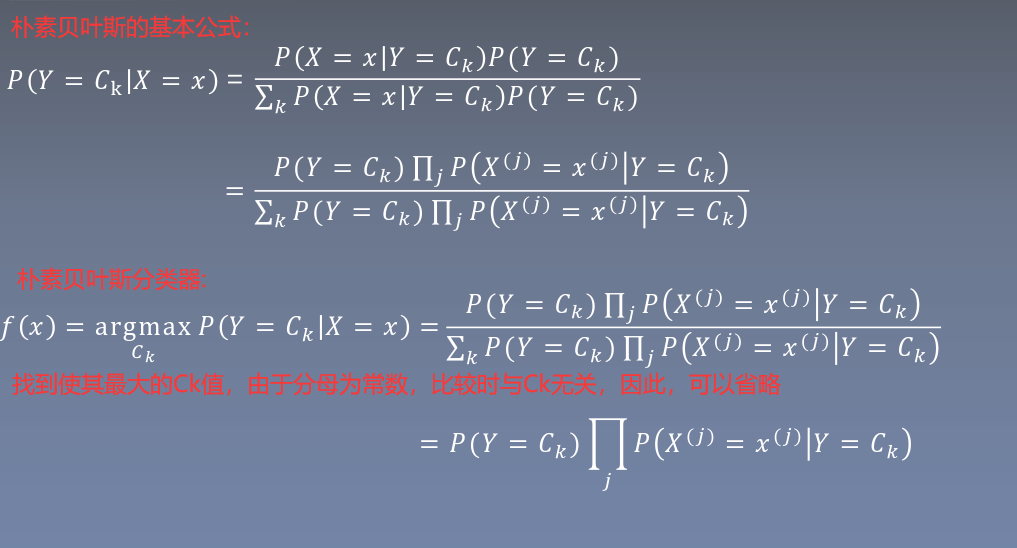統計學習方法第四章樸素貝葉斯
class NaiveBayes:
def __init__(self):
self.model=None
def mean(X):
#數學期望
return sum(X)/float(len(X))
def stdev(self,X):
#求標準差
avg=self.mean(X)
return math.sqrt(sum([pow(X-avg,2) for x in X])) /float(len(X))
def gaussian(self,x,mean,stdev):
#求高斯分布的概率密度函數
resault=math.exp(-(math.pow(x-mean,2)/(2*math.pow(stdev,2))))
return=(1/math.sqrt(2*math.pi)*math.pow(stdev,2))*resault
def summarize(self,train_data):
summarizes=[(self.mean(i),self.stdev(i)) for i in zip(*train_data)]
#zip:壓縮;zip(*train_data):解壓縮。將train_data看作是壓縮之后的元組列表進行解壓
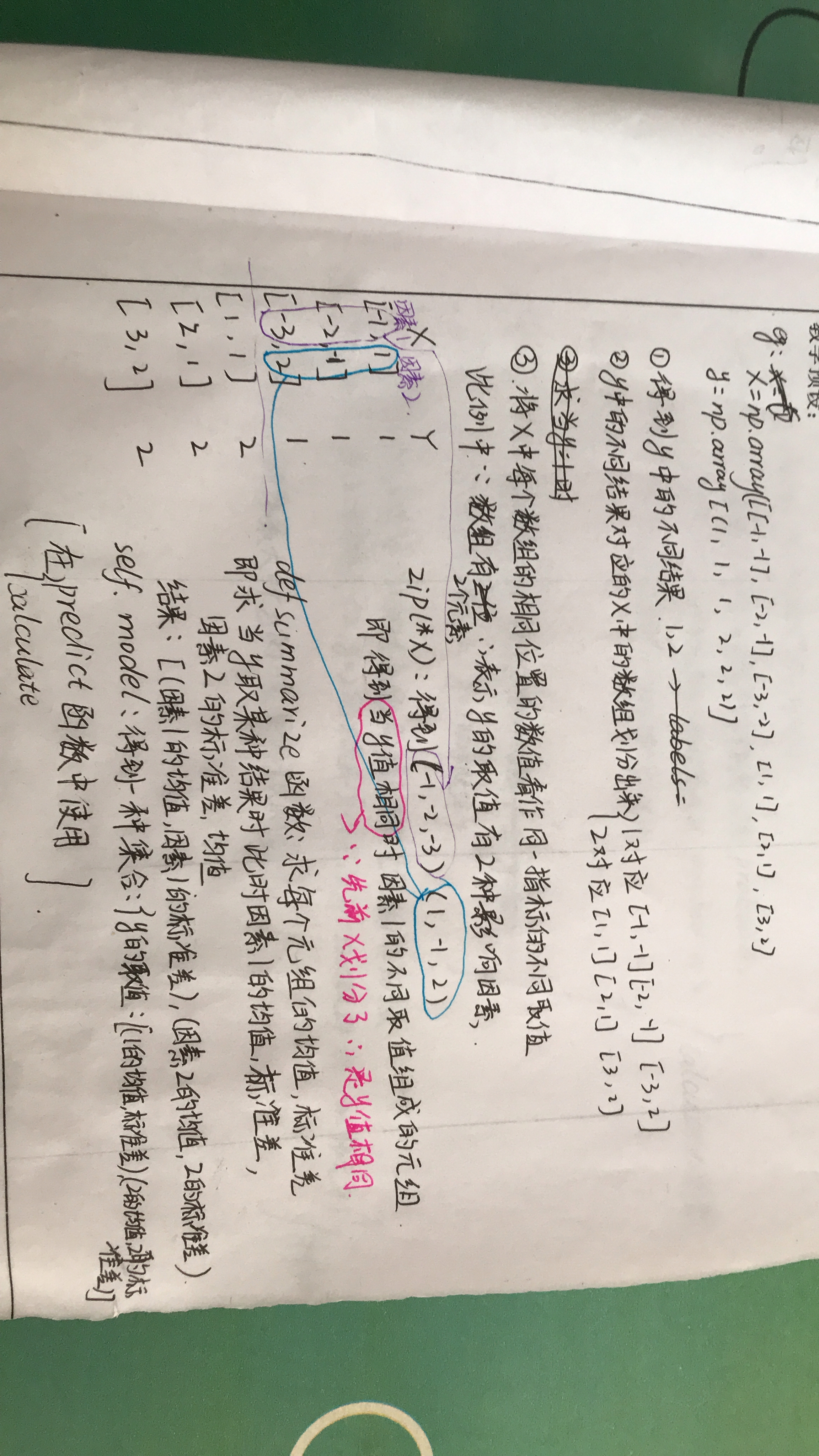
#eg:若train_data= np.array([[-1, -1], [-2, -1], [-3, -2]])
#則zip(*train_data)將每個數組的對應位置的元素取出結果為:(-1,-2,-3){一類y的結果對應的每個數組的第0個元素};
#(-1,-2,1,2){每個數組的第1個元素}且需做去重處理
#得到的結果為: [(-2.0, 0.816496580927726), (-1.3333333333333333, 0.4714045207910317)]
def fit(self,X,y):
labels=list(set(y))
#set() 函數創建集合
#即labels中的元素是y中的所有元素做去重處理得到的
data={label:[] for label in labels}
for f,label in zip(X,y):
data[label].append(f)
#得到的data是一個集合:key:y中的一個元素,value:包含X中的一些數組
#將X中的數組劃分為len(labels)種,第一個label對應的value值是X中的前len(X)/len(label)種
#比如若labels: [1, 2],X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
#則:因為labels含有2個元素,所以將X中的元素劃分為2類,一個label對應一類
#結果:{1:[array([-1, -1]),array([-2, -1]),array([-3, -2])],2:[array([1,1]),array([2,1]),array([3,2])]}
self.model={label:self.summarize(value) for label,value in data.items()}
#得到的data是集合形式,key:labels的值
#value:將每個數組的相同位置看作是一類指標的不同取值,這一類指標的均值和方差組成一個元祖作為value
#延續上面的例子:
#self.model {1: [(-2.0, 0.816496580927726), (-1.3333333333333333, 0.4714045207910317)], 2: [(2.0, 0.816496580927726), (1.3333333333333333, 0.4714045207910317)]}
return 'GaussianNB train done'
def calculate(self,input_data):
#計算概率
probabilities={}
#創建空集合
for label,value in self.model.items():
probabilities[label]=1
for i in range(len(value)):
#求input_data數組的第一個元素的高斯概率結果
#再循環一次求input_data數組的下一個元素的高斯概率結果
#依次循環
mean,stdev=value[i]
probabilities[label]*=self.gaussian(input_data[i],mean,stdev)
return probabilities
def predict(self,X_test):
label=sorted(self.calculate(X_test).items(),key=lambda x:x[-1])[-1][0]
return label
def score(self,X_test,y_test):
right=0
for X,y in zip(X_test,y_test):
label=self.predict(X)
if label==y:
right+=1
return right/float(len(X_test))
# 計算概率
def calculate_probabilities(self, input_data):
probabilities = {}
for label, value in self.model.items():
probabilities[label] = 1
for i in range(len(value)):
mean, stdev = value[i]
probabilities[label] *= self.gaussian_probability(input_data[i], mean, stdev)
#先擬合出一個高斯函數
print('mean',mean)
print('stdev',stdev)
print(probabilities[label])
return probabilities
# 類別
def predict(self, X_test):
label = sorted(self.calculate_probabilities(X_test).items(), key=lambda x: x[-1])[-1][0]
return label
def score(self, X_test, y_test):
right = 0
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right += 1
return right / float(len(X_test))
思路

import math
import numpy as np
class NaiveBayes:
def __init__(self):
self.model = None
# 數學期望
@staticmethod
def mean(X):
return sum(X) / float(len(X))
# 標準差(方差)
def stdev(self, X):
avg = self.mean(X)
return math.sqrt(sum([pow(x-avg, 2) for x in X]) / float(len(X)))
# 概率密度函數
def gaussian_probability(self, x, mean, stdev):
exponent = math.exp(-(math.pow(x-mean,2)/(2*math.pow(stdev,2))))
return (1 / (math.sqrt(2*math.pi) * stdev)) * exponent
# 處理X_train
def summarize(self, train_data):
summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]
for i in zip(*train_data):
print(i)
print('summaries:',summaries)
return summaries
# 分類別求出數學期望和標準差
def fit(self, X, y):
labels = list(set(y))
print('labels:',labels)
data = {label:[] for label in labels}
print('data:',data)
for f, label in zip(X, y):
data[label].append(f)
print('data2:', data)
self.model = {label: self.summarize(value) for label, value in data.items()}
print('self.model',self.model)
return 'GaussianNB train done!'
# 計算概率
def calculate_probabilities(self, input_data):
probabilities = {}
for label, value in self.model.items():
probabilities[label] = 1
for i in range(len(value)):
print('{}'.format(i))
mean, stdev = value[i]
probabilities[label] *= self.gaussian_probability(input_data[i], mean, stdev)
#先擬合出一個高斯函數
print('mean', mean)
print('stdev', stdev)
print('probabilities{}-{}'.format(label,probabilities[label]))
print('******---------------------------------------------------*')
print('probabl:',probabilities)
return probabilities
def predict(self, X_test):
# {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
label = sorted(self.calculate_probabilities(X_test).items(), key=lambda x: x[-1])[-1][0]
print('sort:',sorted(self.calculate_probabilities(X_test).items(), key=lambda x: x[-1]))
print('label',label)
return label
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([1, 1, 1, 2, 2, 2])
input_data= np.array([1.1, 2.2])
model = NaiveBayes()
model.fit(X, Y)
#model.calculate_probabilities(input_data)
model.predict(input_data)
調用包做:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
iris = load_iris()
X = iris.data
Y = iris.target
from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import MultinomialNB
from sklearn.naive_bayes import BernoulliNB
clf=GaussianNB()
clf.fit(X,Y)
iris = load_iris()
X = iris.data
Y = iris.target
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.4, random_state=0)
nb = GaussianNB()
nb.fit(X_train, y_train)
y_pred = nb.fit(iris.data, iris.target).predict(iris.data)
print("Number of mislabeled points out of a total %d points : %d"% (iris.data.shape[0],(iris.target != y_pred).sum()))
print("Naive Gausian bayes score (sklearn): " +str(nb.score(X_test, y_test)))
nb = MultinomialNB()
#假設Y符合樸素多項式的多項式分布
nb.fit(X_train, y_train)
y_pred = nb.fit(iris.data, iris.target).predict(iris.data)
print("Number of mislabeled points out of a total %d points : %d"% (iris.data.shape[0],(iris.target != y_pred).sum()))
print("Naive MultinomialNB() bayes score (sklearn): " +str(nb.score(X_test, y_test)))
nb = BernoulliNB()
#伯努利分布
nb.fit(X_train, y_train)
y_pred = nb.fit(iris.data, iris.target).predict(iris.data)
print("Number of mislabeled points out of a total %d points : %d"% (iris.data.shape[0],(iris.target != y_pred).sum()))
print("Naive BernoulliNB bayes score (sklearn): " +str(nb.score(X_test, y_test)))
智能推薦
統計學習方法學習筆記3——樸素貝葉斯模型
樸素貝葉斯屬于:概率模型、參數化模型、和生成模型 目錄 1.樸素貝葉斯基本方法 2.后驗概率最大化的含義 3.樸素貝葉斯算法: 樸素貝葉斯python實現4.1: 樸素貝葉斯sklearn實現作業4.1 貝葉斯的優缺點: 1.樸素貝葉斯基本方法 2.后驗概率最大化的含義 3.樸素貝葉斯算法: 樸素貝葉斯python實現4.1: 結果: 樸素貝葉斯sklearn實現作業4.1 貝葉斯的優缺點: 由于...
統計學習方法之樸素貝葉斯理解和代碼復現
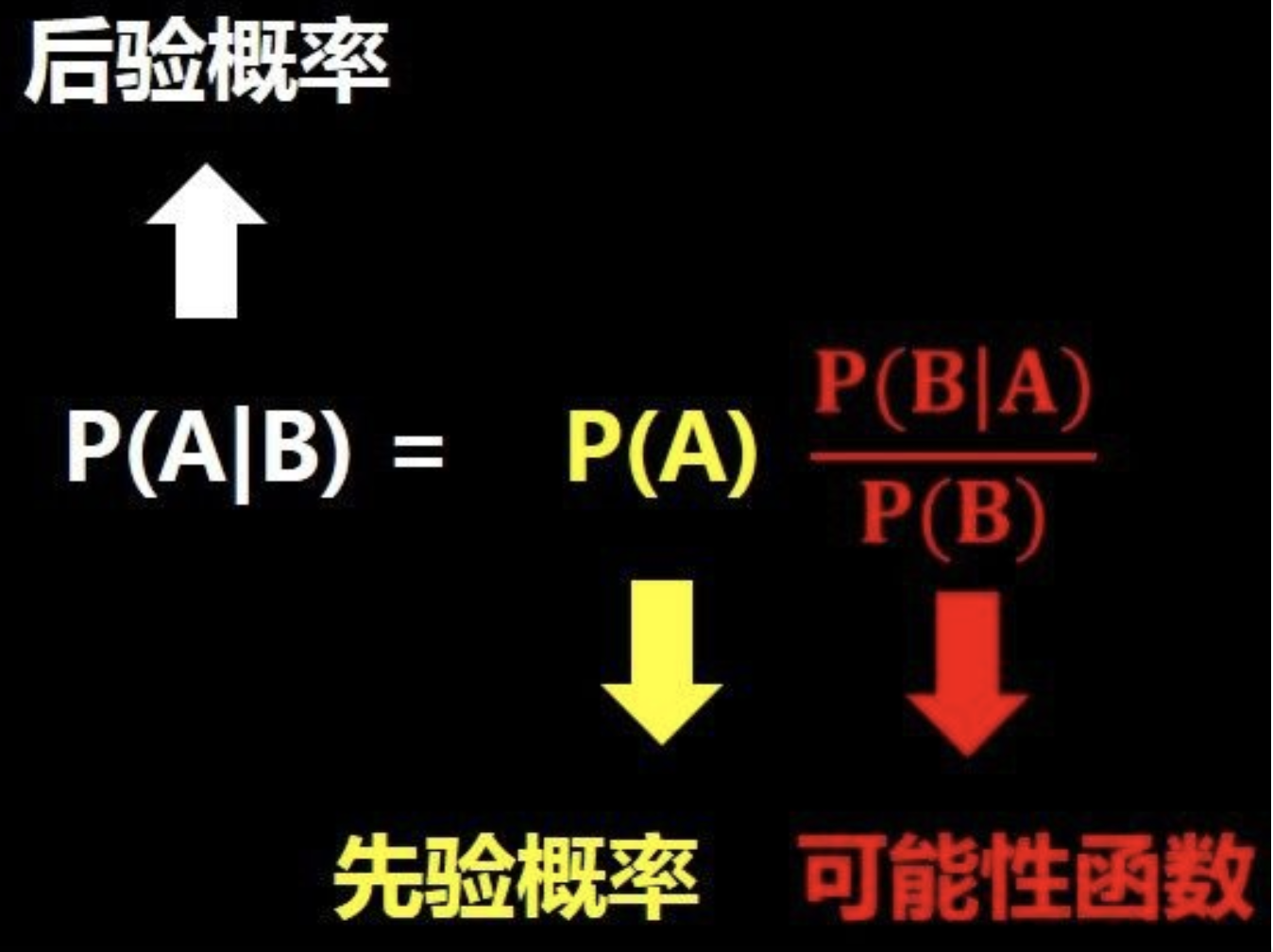
樸素貝葉斯 聯合概率 P(A,B) = P(B|A)*P(A) = P(A|B)*P(B)將右邊兩個式子聯合得到下面的式子: P(A|B)表示在B發生的情況下A發生的概率。P(A|B) = [P(B|A)*P(A)] / P(B) 直觀理解一下這個式子,如下圖,問題A在我們知道B信息之后概率發生了變化(圖片來自于小白之通俗易懂的貝葉斯定理(Bayes’ Theorem) 1.后驗概率推...
統計學習方法-代碼實現-樸素貝葉斯
目錄 貝葉斯定理 樸素貝葉斯算法 貝葉斯估計 代碼實現 貝葉斯定理 其中 所以樸素貝葉斯分類器為 因為分母是一定的,與Y無關,所以簡化為 樸素貝葉斯算法 貝葉斯估計 因為 可能為0,則無法計算 所以將樸素貝葉斯修正為貝葉斯估計 代碼實現...
統計學習方法讀書筆記8-樸素貝葉斯
文章目錄 1.樸素貝葉斯的基本方法 2.樸素貝葉斯的參數估計 1.極大似然估計 2.樸素貝葉斯算法 3.貝葉斯估計 3.后驗概率最大化-期望風險最小化 4.樸素貝葉斯代碼實現 1.樸素貝葉斯的基本方法 2.樸素貝葉斯的參數估計 1.極大似然估計 2.樸素貝葉斯算法 3.貝葉斯估計 用極大似然估計可能出現所要估計的概率值為0的情況,這是會影響到后驗概率的計算結果,使分類產生偏差。解決這一問題的方法就...
樸素貝葉斯(normal bayes)及其應用(MLIA第四章)
1. 概念簡介 貝葉斯(約1701-1761) Thomas Bayes,英國數學家。約1701年出生于倫敦,做過神甫。1742年成為英國皇家學會會員。1761年4月7日逝世。貝葉斯在數學方面主要研究概率論。他首先將歸納推理法用于概率論基礎理論,并創立了貝葉斯統計理論,對于統計決策函數、統計推斷、統計的估算等做出了貢獻。 貝葉斯定理也稱貝葉斯推理,早在18世紀,英國學者貝葉斯(1702~1763)...
猜你喜歡
freemarker + ItextRender 根據模板生成PDF文件
1. 制作模板 2. 獲取模板,并將所獲取的數據加載生成html文件 2. 生成PDF文件 其中由兩個地方需要注意,都是關于獲取文件路徑的問題,由于項目部署的時候是打包成jar包形式,所以在開發過程中時直接安照傳統的獲取方法沒有一點文件,但是當打包后部署,總是出錯。于是參考網上文章,先將文件讀出來到項目的臨時目錄下,然后再按正常方式加載該臨時文件; 還有一個問題至今沒有解決,就是關于生成PDF文件...
電腦空間不夠了?教你一個小秒招快速清理 Docker 占用的磁盤空間!
Docker 很占用空間,每當我們運行容器、拉取鏡像、部署應用、構建自己的鏡像時,我們的磁盤空間會被大量占用。 如果你也被這個問題所困擾,咱們就一起看一下 Docker 是如何使用磁盤空間的,以及如何回收。 docker 占用的空間可以通過下面的命令查看: TYPE 列出了docker 使用磁盤的 4 種類型: Images:所有鏡像占用的空間,包括拉取下來的鏡像,和本地構建的。 Con...
requests實現全自動PPT模板
http://www.1ppt.com/moban/ 可以免費的下載PPT模板,當然如果要人工一個個下,還是挺麻煩的,我們可以利用requests輕松下載 訪問這個主頁,我們可以看到下面的樣式 點每一個PPT模板的圖片,我們可以進入到詳細的信息頁面,翻到下面,我們可以看到對應的下載地址 點擊這個下載的按鈕,我們便可以下載對應的PPT壓縮包 那我們就開始做吧 首先,查看網頁的源代碼,我們可以看到每一...