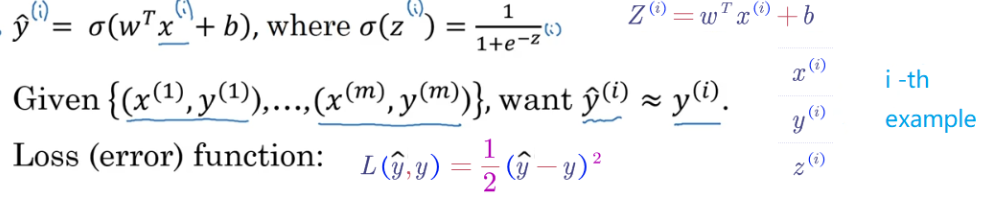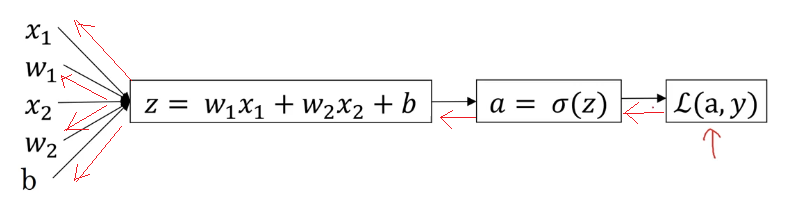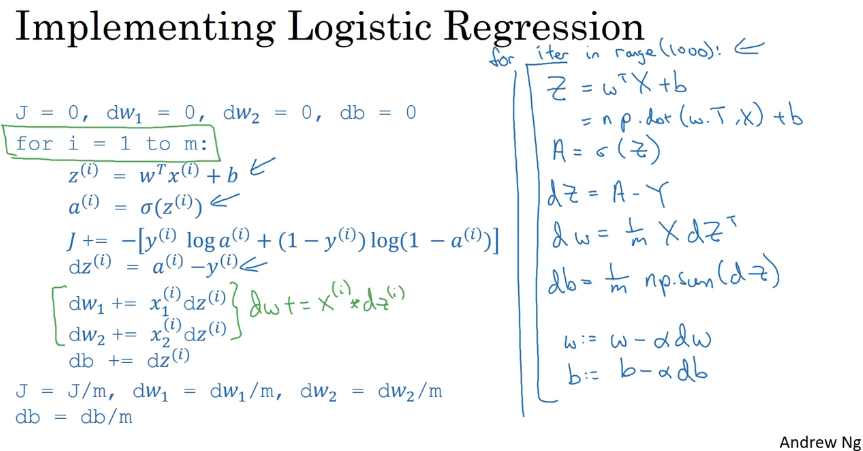在吳恩達深度學習視頻以及大樹先生的博客提煉筆記基礎上添加個人理解，原大樹先生博客可查看該鏈接地址大樹先生的博客- ZJ

Coursera 課程 |deeplearning.ai |網易云課堂

CSDN：http://blog.csdn.net/junjun_zhao/article/details/79226016

---

第二周 神經網絡基礎 (Basics of Neural Network Programming )

2.1 二分分類 ( Binary Classification)

神經網絡編程的基礎知識

例如 m 個樣本的訓練集，你可能會習慣性地去用一個 for 循環，來遍歷這 m 個樣本。實現一個神經網絡，如果你要遍歷整個訓練集，并不需要直接使用 for 循環。

本周介紹為什么神經網絡的計算過程可以分為 前向傳播和反向傳播 兩個分開的過程。 用logistic 回歸 來闡述，以便于更好地理解。

logistic 回歸是一個用于二分分類的算法。

二分分類問題的例子：

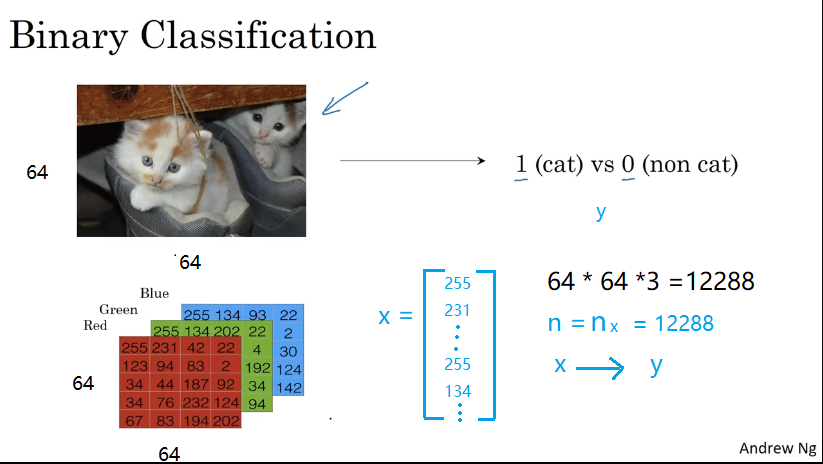
假如你有一張圖片作為輸入，這樣子的，你想輸出識別此圖的標簽，如果是貓 輸出 1，如果不是 則輸出 0，我們用 y 來表示輸出的結果標簽。

一張圖片在計算機中的表示：

三個獨立矩陣，分別對應圖片中的 紅、綠、藍三個顏色通道，如果輸入圖片是 64×64 像素的，就有三個 64×64 的矩陣，分別對應圖片中 紅、綠、藍 三種像素的亮度。放入一個特征向量 x$x$。 向量 x 的總維度 就是 64×64×3=12288

Notation 符號

• 樣本：(x,y)$(x,y)$，訓練樣本包含 m 個；
• 其中x∈Rnx$x\in R^{n_x}$，表示樣本 x 包含nx$n_x$個特征；
• y∈0,1$y\in 0,1$，目標值屬于 0、1分類；
• 訓練數據： {(x(1),y(1)),(x(2),y(2)),?,(x(m),y(m))}$\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),?,(x^{(m)},y^{(m)})\}$

訓練數據樣本形狀： X.shape=(nx,m)$X.shape=(n_x,m)$

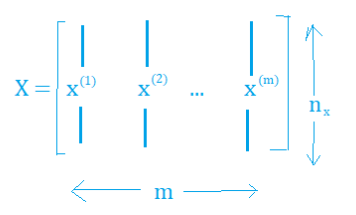
對應標簽數據的形狀：Y=[y(1),y(2),?,y(m)]$Y=[y^{(1)},y^{(2)},?,y^{(m)}]$ , Y.shape=(1,m)$Y.shape=(1,m)$

---

2.2 Logistic 回歸 (Logistic Regression)

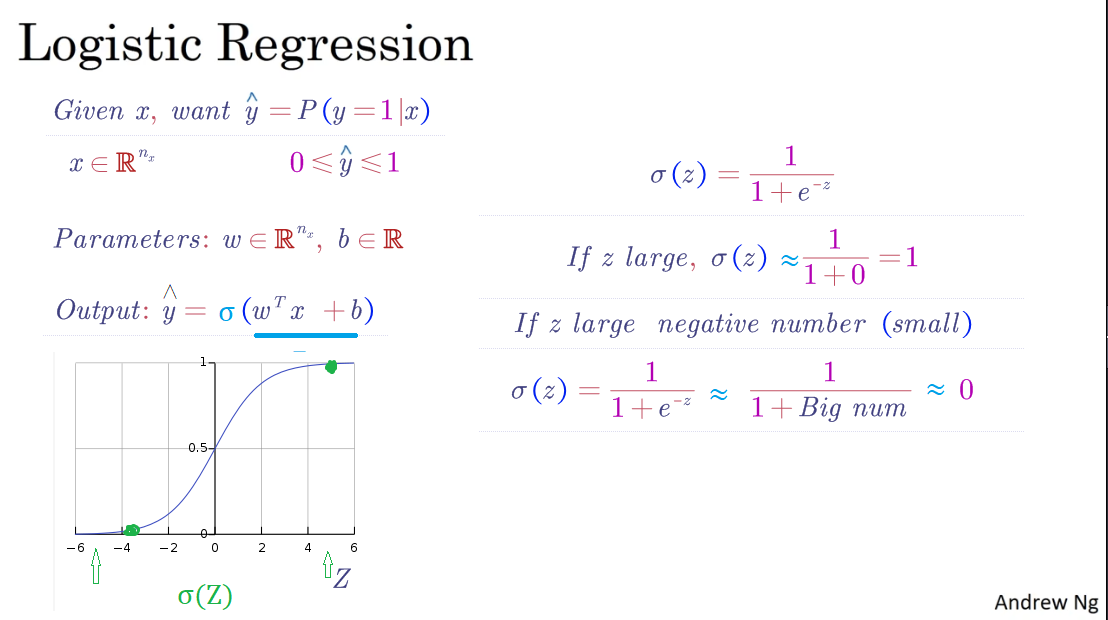
logistic 回歸，用在監督學習問題中的學習算法 ，輸出 y 標簽是 0 或 1 ，這是一個二元分類問題

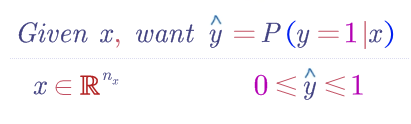
邏輯回歸中，預測值：

h^=P(y=1|x)$\hat{h}=P(y=1|x)$

其表示為 1 的概率，取值范圍在 [0,1] 之間。

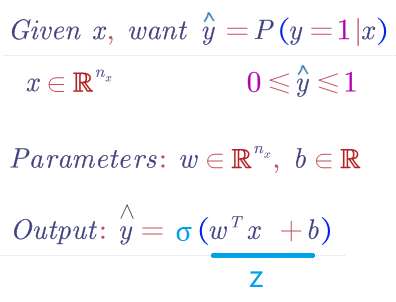
引入 Sigmoid 函數，預測值：

y^=Sigmoid(wTx+b)=σ(wTx+b)$\hat{y}=Sigmoid(w^{T}x+b)=\sigma (w^{T}x+b)$

其中

Sigmoid(z)=11+e?z$Sigmoid(z)={\displaystyle \frac{1}{1+e^{?z}}}$

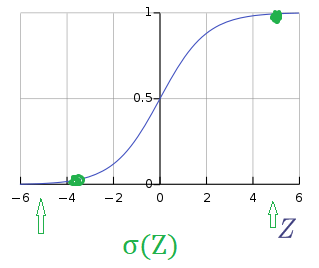
注意點：函數的一階導數可以用其自身表示，

該部分的求導可查看：Logistic回歸-代價函數求導過程 | 內含數學相關基礎

σ′(z)=σ(z)(1?σ(z))${\sigma }^{\prime }(z)=\sigma (z)(1?\sigma (z))$

這里可以解釋梯度消失的問題，當 z=0$z=0$ 時，導數最大，但是導數最大為σ′(0)=σ(0)(1?σ(0))=0.5(1?0.5)=0.25${\sigma }^{\prime }(0)=\sigma (0)(1?\sigma (0))=0.5(1?0.5)=0.25$，這里導數僅為原函數值的 0.25 倍。

---

2.3 Logistic 回歸成本函數 (Logistic Regression Cost function)

logistic 回歸的模型，為了訓練 logistic 回歸模型的參數 w 以及 b，需要定義一個成本函數，用 logistic 回歸來訓練的成本函數。

讓模型來通過學習調整參數:

• m 個樣本的訓練集， 通過在訓練集 找到參數 w 和 b ，得到輸出，對訓練集中的預測值 y^(i)${\hat{y}}^{(i)}$

誤差平方：

一般經驗來說，使用平方錯誤（squared error）來衡量 Loss Function：

L(y^,y)=12(y^?y)2$L(\hat{y},y)={\displaystyle \frac{1}{2}}(\hat{y}?y{)}^2$

注意： 但是，對于 logistic regression 來說，一般不適用平方錯誤來作為 Loss Function，這是因為上面的平方錯誤損失函數一般是非凸函數（non-convex），其在使用梯度下降算法的時候，容易得到多個局部最優解，而不是全局最優解。因此要選擇凸函數。

logistic 回歸的損失函數 （Loss Function）：

Loss=?(y?log(y^)+(1?y)log(1?y^))$Loss=?(y?log(\hat{y})+(1?y)log(1?\hat{y}))$

• 當 y=1$y=1$ 時，L(y^,y)=?logy^$L(\hat{y},y)=?\log ?\hat{y}$。如果 y^$\hat{y}$ 越接近 1，L(y^,y)≈0$L(\hat{y},y)\approx 0$，表示預測效果越好；如果y^$\hat{y}$越接近 0，L(y^,y)≈+∞$L(\hat{y},y)\approx +\mathrm{\infty }$，表示預測效果越差；

• 當 y=0$y=0$ 時，L(y^,y)=?log(1?y^)$L(\hat{y},y)=?\log ?(1?\hat{y})$。如果y^$\hat{y}$越接近0，L(y^,y)≈0$L(\hat{y},y)\approx 0$，表示預測效果越好；如果y^$\hat{y}$越接近1，L(y^,y)≈+∞$L(\hat{y},y)\approx +\mathrm{\infty }$，表示預測效果越差；

• 我們的目標是最小化樣本點的損失 Loss Function，損失函數是針對單個樣本點的。

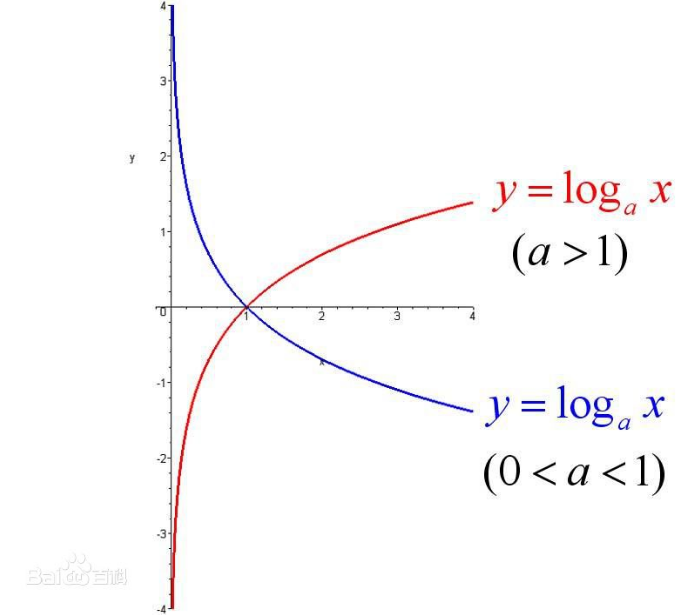
補充 log 函數圖:

損失函數是，在單個訓練樣本中定義的，它衡量了在單個訓練樣本上的表現。

成本函數， 它衡量的是在全體訓練樣本上的表現。

全部訓練數據集的 Loss function 總和的平均值即為訓練集的代價函數（Cost function）。

• Cost function 是待求系數 w 和 b的函數；
• 我們的目標就是迭代計算出最佳的 w 和 b 的值，最小化 Cost function，讓其盡可能地接近于0。

---

2.4 梯度下降法 （Gradient Descent ）

回顧：

1. Loss function (損失函數)：是衡量單一訓練樣本的效果。
2. Cost function (成本函數)：成本函數是在全部訓練集上，來衡量參數 w 和 b 的效果。

如何使用梯度下降法來訓練或學習訓練集上的參數 w 和 b

1.Logistic 回歸：

y^=σ(wTx+b)$\hat{y}=\sigma (w^{T}x+b)$, σ(z)=11+e?z$\sigma (z)={\displaystyle \frac{1}{1+e^{?z}}}$ ,z=wTx+b$z=w^{T}x+b$

2.Cost function (成本函數)：

J(w,b)=1m∑mi=1L(y^(i),y(i))=?1m∑mi=1[y(i)logy^(i)+(1?y(i))log(1?y^(i))]$J(w,b)={\displaystyle \frac{1}{m}}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})=?{\displaystyle \frac{1}{m}}\sum _{i=1}^m\left[y^{(i)}\log ?{\hat{y}}^{(i)}+(1?y^{(i)})\log ?(1?{\hat{y}}^{(i)})\right]$

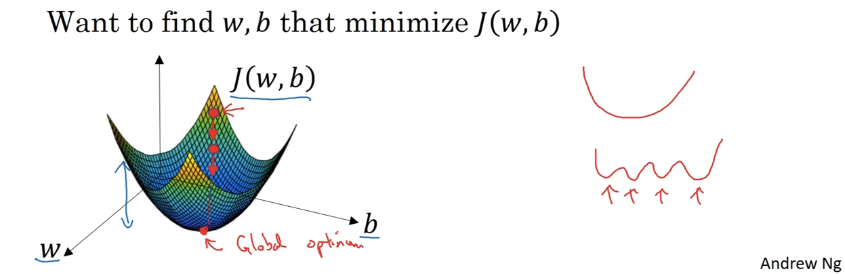
目的：找到（學習訓練得到）w and b ，使得成本函數J(w,b)$J(w,b)$最小。

凸函數：全局最優解。(這是我們想要的)
非凸函數：局部最優解。

w:=w?α?J(w,b)?w$w:=w?\alpha {\displaystyle \frac{\mathrm{?}J(w,b)}{\mathrm{?}w}}$

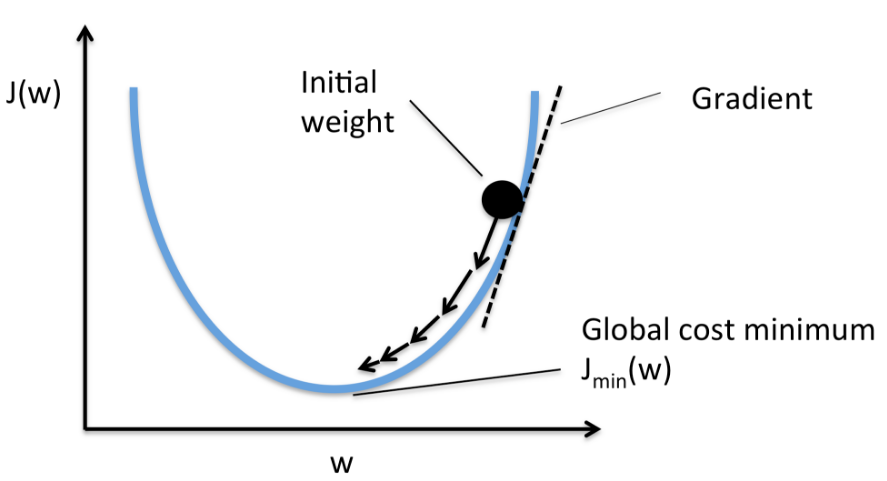
學習率 learning_rate ：α$\alpha$

我們用 dw，作為導數的變量名，現在我們確保梯度下降法更新是有用的。w 在這對應的成本函數 J(w) 在曲線上的這一點。記住導數的定義，是函數在這個點的斜率，而函數的斜率是高除以寬。

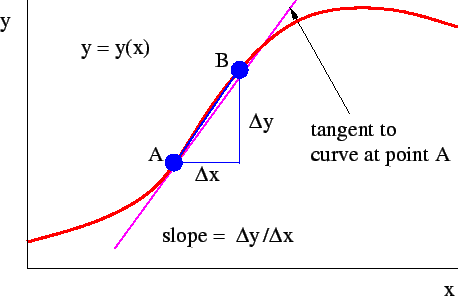
無論你初始化的位置是在左邊還是右邊，梯度下降法會朝著全局最小值方向移動

梯度下降法

用梯度下降法（Gradient Descent）算法來最小化 Cost function，以計算出合適的 w 和 b 的值。

迭代更新的修正表達式：

w:=w?α?J(w,b)?w$w:=w?\alpha {\displaystyle \frac{\mathrm{?}J(w,b)}{\mathrm{?}w}}$

b:=b?α?J(w,b)?b$b:=b?\alpha {\displaystyle \frac{\mathrm{?}J(w,b)}{\mathrm{?}b}}$

在程序代碼中，我們通常使用 dw$dw$ 來表示?J(w,b)?w${\displaystyle \frac{\mathrm{?}J(w,b)}{\mathrm{?}w}}$，用 db$db$ 來表示?J(w,b)?b${\displaystyle \frac{\mathrm{?}J(w,b)}{\mathrm{?}b}}$。

偏導數符號 使用 ?$\mathrm{?}$ 還是小寫字母 d$d$：取決于你的函數 J 是否含有兩個以上的變量 :

1. 變量超過兩個就用偏導數符號 ?$\mathrm{?}$ ，
2. 如果函數只有一個變量就用小寫字母 d。

---

2.5 導數（Derivatives）

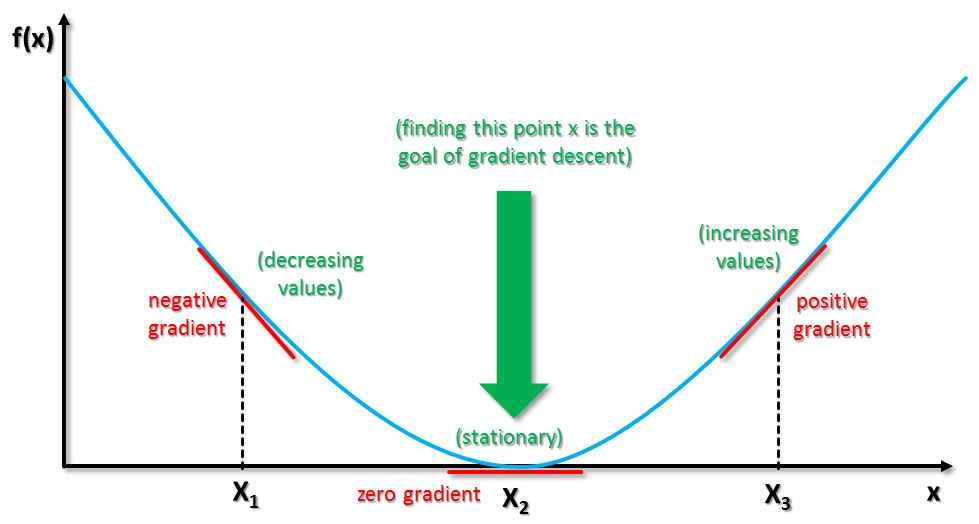
導數，函數的斜率，斜率定義， 高除以寬。

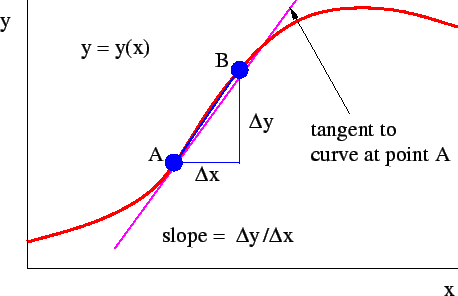
【wiki | 導數】:https://zh.wikipedia.org/wiki/%E5%AF%BC%E6%95%B0

---

2.6 更多導數的例子 (More derivatives examples)

重點：

1. 函數的導數，就是函數的斜率，而函數的斜率在不同的點是不同的。
2. 如果你想知道 一個函數的導數，你可參考微積分課本或者維基百科，然后你應該就能，找到這些函數的導數公式。

---

2.7 計算圖 （Computation Graph）

一個神經網絡的計算，都是按照前向或反向傳播過程來實現的。

---

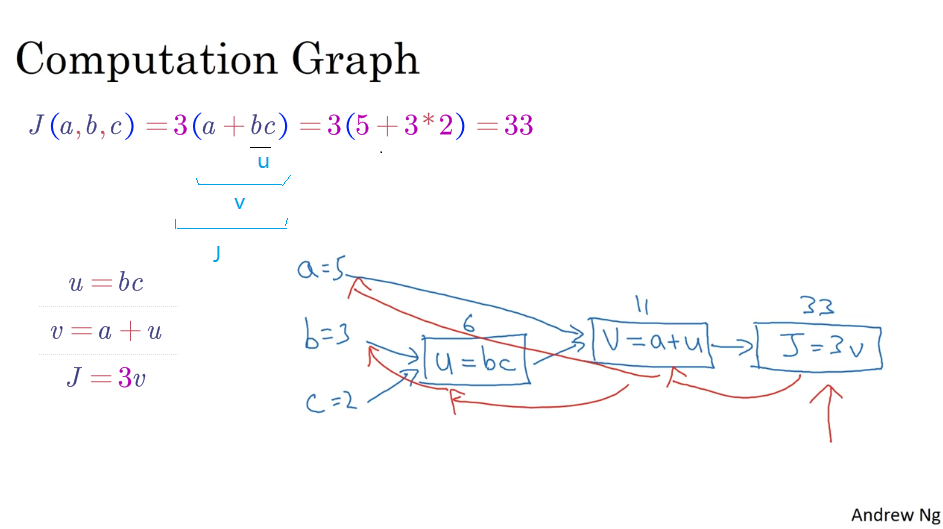
2.8 計算圖的導數計算 （Derivatives with a Computation Graph ）

---

2.9 logistic 回歸中的梯度下降法 （Logistic Regression Gradient Descent）

對單個樣本而言，邏輯回歸 Loss function 表達式：

z=wTx+by^=a=σ(z)L(a,y)=?(ylog(a)+(1?y)log(1?a))$$\begin{gathered} z=w^{T}x+b \\ \hat{y}=a=\sigma (z) \\ L(a,y)=?(y\log ?(a)+(1?y)\log ?(1?a)) \end{gathered}$$

反向傳播過程：（紅色部分）

前面過程的 da$da$、dz$dz$ 求導：

da=?L?a=?ya+1?y1?adz=?L?z=?L?a??a?z=(?ya+1?y1?a)?a(1?a)=a?y$$\begin{gathered} da={\displaystyle \frac{\mathrm{?}L}{\mathrm{?}a}}=?{\displaystyle \frac{y}{a}}+{\displaystyle \frac{1?y}{1?a}} \\ dz={\displaystyle \frac{\mathrm{?}L}{\mathrm{?}z}}={\displaystyle \frac{\mathrm{?}L}{\mathrm{?}a}}?{\displaystyle \frac{\mathrm{?}a}{\mathrm{?}z}}=(?{\displaystyle \frac{y}{a}}+{\displaystyle \frac{1?y}{1?a}})?a(1?a)=a?y \end{gathered}$$

再對w1、w2和b$w1、w2和b$進行求導：

dw1=?L?w1=?L?z??z?w1=x1?dz=x1(a?y)$d{w}_1={\displaystyle \frac{\mathrm{?}L}{\mathrm{?}{w}_1}}={\displaystyle \frac{\mathrm{?}L}{\mathrm{?}z}}?{\displaystyle \frac{\mathrm{?}z}{\mathrm{?}{w}_1}}=x_1?dz=x_1(a?y)$

梯度下降法：

w1:=w1?αdw1$w_1:=w_1?\alpha d{w}_1$

w2:=w2?αdw2$w_2:=w_2?\alpha d{w}_2$

b:=b?αdb$b:=b?\alpha db$

---

2.10 m 個樣本的梯度下降 （Gradient Descent on m examples）

m 個樣本的梯度下降

對 m 個樣本來說，其 Cost function 表達式如下：

z(i)=wTx(i)+by^(i)=a(i)=σ(z(i))J(w,b)=1m∑mi=1L(y^(i),y(i))=?1m∑mi=1[y(i)logy^(i)+(1?y(i))log(1?y^(i))]$$\begin{gathered} z^{(i)}=w^T{x}^{(i)}+b \\ {\hat{y}}^{(i)}=a^{(i)}=\sigma (z^{(i)}) \\ J(w,b)={\displaystyle \frac{1}{m}}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})=?{\displaystyle \frac{1}{m}}\sum _{i=1}^m\left[y^{(i)}\log ?{\hat{y}}^{(i)}+(1?y^{(i)})\log ?(1?{\hat{y}}^{(i)})\right] \end{gathered}$$

Cost function 關于w和b的偏導數可以寫成所有樣本點偏導數和的平均形式：

dw1=1m∑mi=1x(i)1(a(i)?y(i))$d{w}_1={\displaystyle \frac{1}{m}}\sum _{i=1}^m{x}_1^{(i)}(a^{(i)}?y^{(i)})$

db=1m∑mi=1(a(i)?y(i))$db={\displaystyle \frac{1}{m}}\sum _{i=1}^m(a^{(i)}?y^{(i)})$

---

2.11 （向量化） Vectorization

向量化（Vectorization）

在深度學習的算法中，我們通常擁有大量的數據，在程序的編寫過程中，應該盡最大可能的少使用 loop 循環語句，利用 python 可以實現矩陣運算，進而來提高程序的運行速度，避免 for 循環的使用。

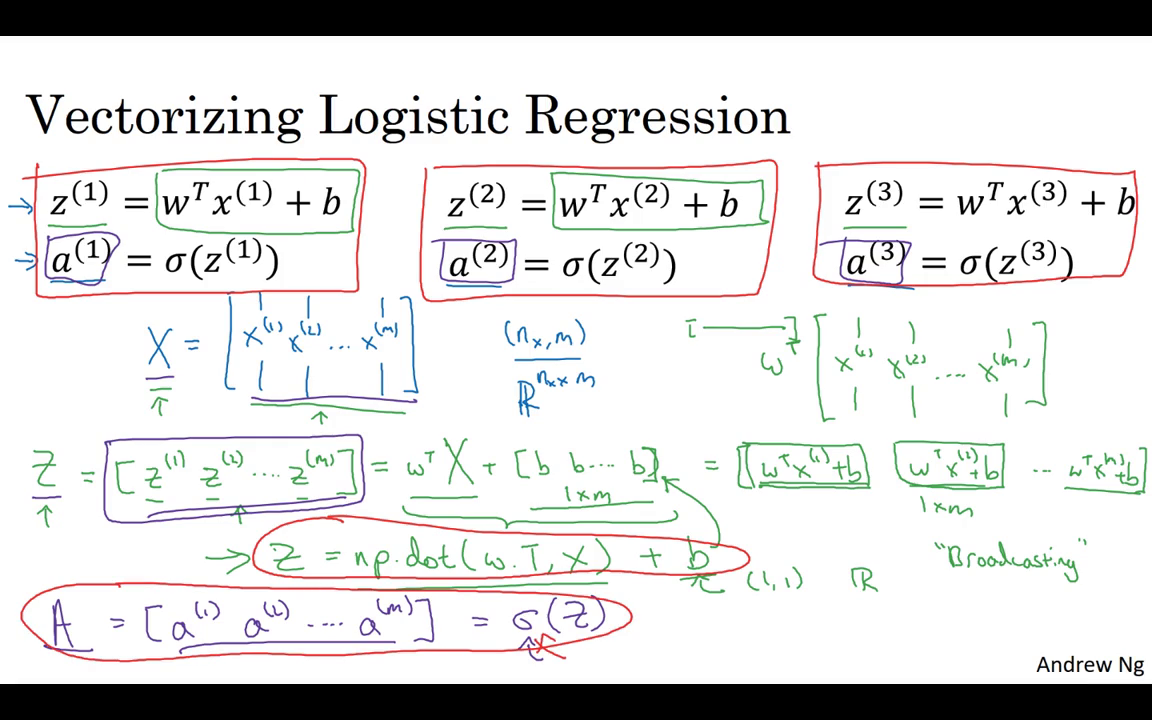
邏輯回歸向量化

• 輸入矩陣X$X$：（nx,m）$（n_x,m）$
• 權重矩陣w$w$：（nx,1）$（n_x,1）$
• 偏置b$b$：為一個常數
• 輸出矩陣Y$Y$：（1,m）$（1,m）$

所有 m 個樣本的線性輸出 Z 可以用矩陣表示：

Z=wTX+b$Z=w^{T}X+b$

Z = np.dot(w.T,X) + b
A = sigmoid(Z)

import numpy as np 

# 2.11  Vectorization| 向量化 --Andrew Ng 

a = np.array([1,2,3,4,5])

print(a)

# [1 2 3 4 5]
# [Finished in 0.3s]

import time

# 隨機創建 百萬維度的數組 1000000 個數據
a = np.random.rand(1000000)
b = np.random.rand(1000000)

# 記錄當前時間 
tic = time.time()

# 執行計算代碼 2 個數組相乘
c = np.dot(a,b)

# 再次記錄時間
toc = time.time()

# str(1000*(toc-tic)) 計算運行之間 * 1000 毫秒級
print('Vectorization vresion:',str(1000*(toc-tic)),' ms')
print(c)
# Vectorization vresion: 6.009101867675781  ms
# [Finished in 1.1s]

c = 0
tic = time.time()
for i in range(1000000):
    c += a[i]*b[i]
toc = time.time()
print(c)

print('For loop :',str(1000*(toc-tic)),' ms')
# For loop : 588.9410972595215  ms
# c= 249960.353586
# NOTE: It is obvious that the for loop method  is too slow

---

2.12 更多向量化的例子 (More Vectorization examples)

---

2.13 向量化 Logistic 回歸 (Vectorizing Logistic Regression )

---

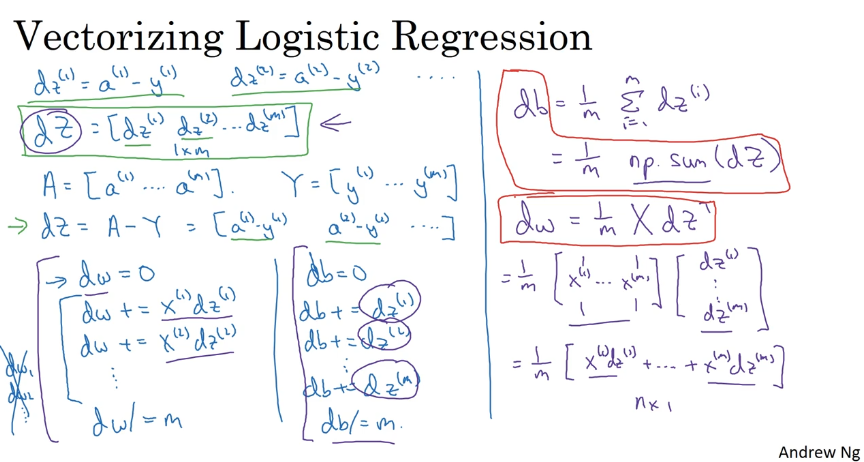
2.14 向量化 logistic 回歸的梯度輸出

Vectorizing Logistic Regression’s Gradient Computation

所有 m 個樣本的線性輸出 Z$Z$ 可以用矩陣表示：

Z=wTX+b$Z=w^{T}X+b$

Z = np.dot(w.T,X) + b
A = sigmoid(Z)

邏輯回歸梯度下降輸出向量化

• dZ$dZ$對于m$m$個樣本，維度為（1,m）$（1,m）$，表示為：

  dZ=A?Y$dZ=A?Y$

• db可以表示為：

db=1m∑mi=1dz(i)$db={\displaystyle \frac{1}{m}}\sum _{i=1}^{m}d{z}^{(i)}$

 db = 1/m * np.sum(dZ)

• dw可表示為：

dw=1mX?dZT$dw={\displaystyle \frac{1}{m}}X?d{Z}^T$

dw = 1/m*np.dot(X,dZ.T)

單次迭代梯度下降算法流程:

Z = np.dot(w.T,X) + b
A = sigmoid(Z)
dZ = A-Y
dw = 1/m*np.dot(X,dZ.T)
db = 1/m*np.sum(dZ)

w = w - alpha*dw
b = b - alpha*db

---

2.15 Python 中的廣播（Boadcasting in Python ）

import numpy as np

# 2.15 Boradcasting in python

A = np.mat([[56.0, 0.0, 4.4, 68.0],
            [1.2, 104.0, 52.0, 8.0],
            [1.8, 135.0, 99.0, 0.9]])
print(A)

# axis=0 代表豎直方向（的數據）相加，最后列數不變，行數變化
cal = A.sum(axis=0)
print(cal)
# [[  59.   239.   155.4   76.9]]

# print("cal.reshape(1,4)",cal.reshape(1,4))
# A/cal 相當于（換算百分比） 100* （56/59） = 94.915 
# A 矩陣中的每一個元素，與當前所在列的總和相除
# cal 根據上面的計算本身就是 1 *4 矩陣，所以cal.reshape(1,4) 這個可以不用
percentage = 100 * A / (cal.reshape(1, 4))
print('percentage=', percentage)

# [[ 94.91525424   0.           2.83140283  88.42652796]
#  [  2.03389831  43.51464435  33.46203346  10.40312094]
#  [  3.05084746  56.48535565  63.70656371   1.17035111]]

---

2.16 關于 python _ numpy 向量的說明(A note on Python_numpy vectors)

# 2.16 A note on python/numpy vectors

# 產生隨機 5 個高斯變量存儲在 a 中
# 官方文檔中給出的用法是：numpy.random.rand(d0,d1,…dn) 
# 以給定的形狀創建一個數組，數組元素來符合標準正態分布N(0,1) 
# 若要獲得一般正態分布N(μ,σ^2) 描述則可用sigma * np.random.randn(…) + mu進行表示 

a = np.random.randn(5)
print('a=', a)
# [-0.23427061 -0.79637413 -0.06117785  0.15440186 -1.43061057]

# a 的大小 
print(a.shape)
# (5,)

# a 的轉置 ，
print(a.T)
# [-0.5694968  -0.23773807 -0.08906264  0.87211753 -0.08380342]

# a 和 a 轉置的內積
print(np.dot(a, a.T))
# 1.15639015502

# 因為 a.shape (5,) 不規范

# tips tricks 技巧，若要生成隨機數組 給出指定的 行列向量

b = np.random.randn(5, 1)
print(b)
# 這是標準的 5 * 1 的列向量
# [[ 0.10087547]
#  [-1.2177768 ]
#  [ 1.55482844]
#  [ 1.39440708]
#  [-1.72344715]]
print(b.T)
# 這是標準的 1 * 5 的行向量
# [[ 0.10087547 -1.2177768   1.55482844  1.39440708 -1.72344715]]
# 5 *1  乘以 1 *5 得到的是一個矩陣 5*5
print(np.dot(b, b.T))
# [[ 0.08517485  0.38272589 -0.11342526  0.23506654  0.16852131]
#  [ 0.38272589  1.71974596 -0.5096667   1.05625134  0.75723604]
#  [-0.11342526 -0.5096667   0.15104565 -0.31303236 -0.2244157 ]
#  [ 0.23506654  1.05625134 -0.31303236  0.64873937  0.46508706]
#  [ 0.16852131  0.75723604 -0.2244157   0.46508706  0.33342507]]


# >>> a = np.mat([[1],[2],[3],[4],[5]])
# >>> b = np.mat([[2,2,2,2,2]])
# >>> c = np.dot(a,b)
# >>> c
# matrix([[ 2,  2,  2,  2,  2],
#         [ 4,  4,  4,  4,  4],
#         [ 6,  6,  6,  6,  6],
#         [ 8,  8,  8,  8,  8],
#         [10, 10, 10, 10, 10]])

• 雖然在 Python 有廣播的機制，但是在 Python 程序中，為了保證矩陣運算的正確性，可以使用reshape()函數來對矩陣設定所需要進行計算的維度，這是個好的習慣；

• 如果用下列語句來定義一個向量，則這條語句生成的 a 的維度為（5，），既不是行向量也不是列向量，稱為秩（rank）為 1 的 array，如果對 a 進行轉置，則會得到 a 本身，這在計算中會給我們帶來一些問題。

a = np.random.randn(5)

• 如果需要定義（5，1）或者（1，5）向量，要使用下面標準的語句：

a = np.random.randn(5,1)
b = np.random.randn(1,5)

• 可以使用assert語句對向量或數組的維度進行判斷。assert會對內嵌語句進行判斷，即判斷 a 的維度是不是（5，1），如果不是，則程序在此處停止。使用assert語句也是一種很好的習慣，能夠幫助我們及時檢查、發現語句是否正確。

assert(a.shape == (5,1))

• 可以使用reshape函數對數組設定所需的維度

a.reshape((5,1))

---

2.17 Jupyter _ ipython 筆記本的快速指南 (Quick tour of Jupyter/ipython notebooks)

Windows jupyter install (Python) 本地搭建

pip3 install jupyter

啟動 jupyter notebook 命令 cmd

jupyter notebook

mac 啟動

jupyter-notebook

---

2.18 logistic 損失函數的解釋 (Explanation of logistic Regression cost function)

logistic$logistic$ regression 代價函數的解釋：

Cost function的由來：

預測輸出y^的表達式：

y^=σ(wTx+b)$\hat{y}=\sigma (w^{T}x+b)$

其中，

σ(z)=11+e?z$\sigma (z)={\displaystyle \frac{1}{1+e^{?z}}}$

y^$\hat{y}$ 可以看作預測輸出為正類（+1）的概率：

y^=P(y=1|x)$\hat{y}=P(y=1|x)$

當 y=1$y=1$時，P(y|x)=y^$P(y|x)=\hat{y}$；
當y=0$y=0$時，P(y|x)=1?y^$P(y|x)=1?\hat{y}$。

將兩種情況整合到一個式子中，可得：

P(y|x)=y^y(1?y^)(1?y)$P(y|x)={\hat{y}}^y(1?\hat{y}{)}^{(1?y)}$

對上式進行 log$log$ 處理（這里是因為 log$log$ 函數是單調函數，不會改變原函數的單調性）：

logP(y|x)=log[y^y(1?y^)(1?y)]=ylogy^+(1?y)log(1?y^)$\log ?P(y|x)=\log ?\left[{\hat{y}}^y(1?\hat{y}{)}^{(1?y)}\right]=y\log ?\hat{y}+(1?y)\log ?(1?\hat{y})$

概率P(y|x)$P(y|x)$越大越好，即判斷正確的概率越大越好。這里對上式加上負號，則轉化成了單個樣本的 Loss function，我們期望其值越小越好：

L(y^,y)=?(ylogy^+(1?y)log(1?y^))$L(\hat{y},y)=?(y\log ?\hat{y}+(1?y)\log ?(1?\hat{y}))$

對于 m 個訓練樣本來說，假設樣本之間是獨立同分布的，我們總是希望訓練樣本判斷正確的概率越大越好，則有：

max∏i=1mP(y(i)|x(i))$max\prod _{i=1}^{m}P(y^{(i)}|x^{(i)})$

同樣引入 log 函數，加負號，則可以得到 Cost function：

J(w,b)=1m∑mi=1L(y^(i),y(i))=?1m∑mi=1[y(i)logy^(i)+(1?y(i))log(1?y^(i))]$J(w,b)={\displaystyle \frac{1}{m}}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})=?{\displaystyle \frac{1}{m}}\sum _{i=1}^m\left[y^{(i)}\log ?{\hat{y}}^{(i)}+(1?y^{(i)})\log ?(1?{\hat{y}}^{(i)})\right]$

參考文獻：

[1]. 大樹先生.吳恩達Coursera深度學習課程 DeepLearning.ai 提煉筆記（1-2）– 神經網絡基礎

---

PS: 歡迎掃碼關注公眾號：「SelfImprovementLab」！專注「深度學習」，「機器學習」，「人工智能」。以及 「早起」，「閱讀」，「運動」，「英語 」「其他」不定期建群 打卡互助活動。