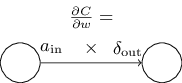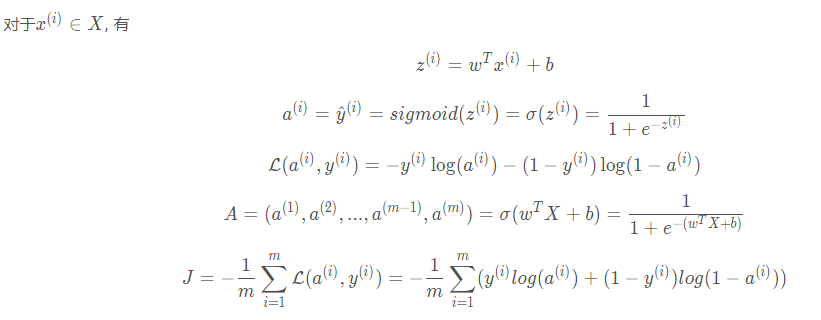TensorFlow官方教程《Neural Networks and Deep Learning》譯(第二章)
反向傳播算法(BackPropagation algorithm)的工作原理
在上一章節中, 我們看到了神經網絡是如何利用梯度下降算法從數據中學習權重值 weights 和 偏倚量值 biases ,完成“學習” 的過程。 但是, 在算法原理的解釋中, 有一個環節被跳過了: 我們沒有討論如何計算成本函數(cost function) 的梯度值。 這是很重要的一個環節! 在這一章, 我們會解釋一個快速計算這種梯度的算法, 名為“反向傳播算法”(BackPropagation algorithm)。
反向傳播算法原本是 19世紀70年代提出的, 但是其重要性直到 1986 年的一篇由(David Rumelhart , Geoffrey Hinton, Ronald Williams 三人所寫的一篇著名論文發布以后才真正被世人意識到。這篇論文描述了幾個神經網絡在使用了反向傳播算法以后, 學習速度比之前有顯著提升, 使得用這些神經網絡來解決以前看上去不可解的問題成為可能。 如今, 反向傳播算法已經成為了神經網絡進行學習的“核心骨干”算法。
本章節與本書的其余章節相比涉及了更多數學上的內容。 如果你對數學不是很熱衷, 你可能會想要跳過這一章節, 然后把反向傳播算法當做一個忽略其內部細節的黑盒來使用。 但是為什么我們要花費時間來學習這些細節呢?
原因當然是為了“弄懂”。 反向傳播算法 核心是一個成本函數
雖然說了上面這一大堆, 如果你依舊只是想略讀這一章,或是直接跳過這一章, 也是ok的。 本書的其余章節在寫作時, 已經考慮到了你有可能跳過本章, 直接將反向傳播算法當做一個黑盒的情況。所以即使你不略過了本章, 你依舊可以理解后續章節的主要結論, 盡管你可能無法完全跟的上其中的推導過程。
熱身: 一個快速的基于矩陣計算神經網絡輸出的方法
在討論反向傳播算法前, 讓我用一個基于矩陣計算神將網絡輸出的算法熱個身。 事實上, 在上一章結尾, 我們已經初步見識過這一算法了, 但是當時我快速的一帶而過了, 所以值得再重新探究一下其中的細節。 這是一個讓我們逐漸熟悉反向傳播算法中所使用數學記號的很好的方式。
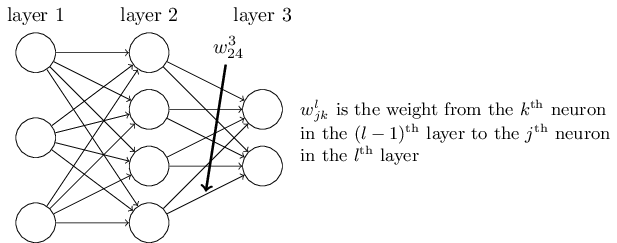
讓我們從一個讓人感到含糊不清的指代神經網絡眾多權重的記號開始。 我們會用
這個記號乍一看是讓人很不習慣的, 它確實需要花費一些功夫來掌握。 但是經過較小的努力之后, 你會發現這個記號變得簡單和自然起來。 這個記號的一個古怪之處在于
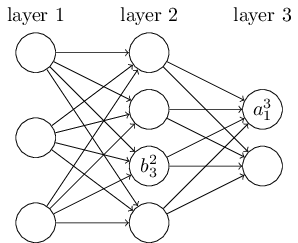
我們使用一個類似的記號來表示神經網絡的偏倚量(biases)和**結果( activations) 。我們用
利用這些記號, 第
上面等式中的
等式 (23) 中最后一個需要重寫的部分就是把
向量化后的
有了這些記號, 等式 (23) 就可以被重寫為非常漂亮可以被重寫為漂亮且緊湊的向量形式:
這個表達式給了我們一個從全局角度思考一層神經元的**結果是如何與前一層神經元的**結果進行關聯的:* 在**結果上乘以權重矩陣, 然后與偏倚量向量相加, 然后再應用
*注釋:
這種全局的視角與之前以神經元為單位的思考更簡單, 更精煉(同時涉及到更少的上下標)。 把它當做是一種避免繁瑣上下標, 且不失準確性的表達技巧。 這種表達式在實踐中也很有用, 因為大部分的矩陣運算庫提供了矩陣乘法, 向量加法, 向量化的快速實現方法。 事實上, 上一章節的代碼
已經隱含地使用了上面那個表達式來計算神經網絡的行為。
在使用表達式【25】來計算
兩個我們所需的關于成本函數的假設
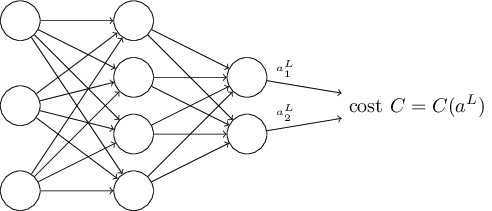
反向傳播函數的目標是計算成本函數
我們會使用上一張提到的二次成本函數作為示例(等式【6】)。 在上一節的記號中, 二次成本函數有如下的形式:
其中:
好的, 那么我們為了成本函數
我們之所以需要這個假設, 是因為反向傳播讓我們做的實際上是計算單個輸入的偏導數
我們所需要做的第二個假設是, 成本可以被寫作神經網絡輸出的一個函數計算結果:
例如, 二次成本函數就滿足這個要求, 因為單個輸入
而且因此, 也就是**結果輸出的一個函數。 當然, 這個成本函數的結果也取決于目標輸出
Hadmard 積, s⊙t
f反向傳播算法是基于常見的線性代數運算的- 如向量加法, 向量與矩陣的乘法等等。 但是, 有一個運算符沒有那么常見。 具體而言, 假設
的內容就是
這種按元素相乘的乘法有時被稱為 Hadmard(哈達瑪達 )乘積 或是 Schur 積, 這個運算符在實現反向傳播算法時會顯得很好用。
反向傳播算法背后的四個基本等式
反向傳播算法幫我們理解神經網絡中權重和偏倚量的變動是如何影響成本函數結果變化的。 最終, 是通過計算偏導數
為了理解這個偏差值是如何被定義的, 先想象我們的神經網絡中有一個惡魔:
這個小惡魔坐在第
。
譯者注: 最后的這個改變量是一個偏微分表達式, 忘記的同學可以復習一下大學課本。
現在這個惡魔變成了一個好的惡魔, 并且試圖幫助你來改善成本值, 也就是說, 他們將試著找到一個
受到這個故事的啟發, 我們定義第
按照我們的慣例, 我們用
你可能在想,為什么小惡魔會更改權重化輸入
【】注釋: 在類似 MNIST 類似的分類問題中, 術語 “誤差”有時被用來表示分類失敗率。 例如, 如果神經網絡正確的識別了 96%的數字,那么誤差就是 4% 。 顯示這和我們的誤差向量
攻擊計劃: 反向傳播算法是基于 4 個基礎等式。 這些等式合起來給了我們一個計算誤差
這里先預覽一下我們在本章后面的部分將要深入鉆研方程的路線:我會給一個等式的簡短證明,以解釋這些等式為什么成立; 我會將這些等式以偽代碼的算法形式再次列出, 看這些偽代碼如何被實現為真正的, 可運行的 python 代碼。 然后, 在這一章的最后一節, 我會構建一個反向傳播算法等式含義的直覺圖, 以及一個怎樣能夠從無到有的發現這個等式。 沿著這條路線, 我們將會反復地審視這四個基礎等式, 而你會不斷加深對它們的理解, 最終你會熟悉習慣這四個等式,甚至可能發覺這四個等式是漂亮且自然的。
首先是一個關于輸出層誤差量的等式
這是一個非常自然的等式, 等式右側的
注意到 (BP1 ) 中的每個部分都是易于計算的。 具體來說, 我們在計算神經網絡的行為時, 會計算
譯者注: 又需要復習一下高數里的微分部分。
等式 (BP1) 是一個關于
這里,
如你所見, 這個表達式中的每個部分都有一個非常簡潔的向量形式, 而且很容易使用類似 Numpy 的庫進行計算。
等式 (BP2) 是是關于誤差量
其中,
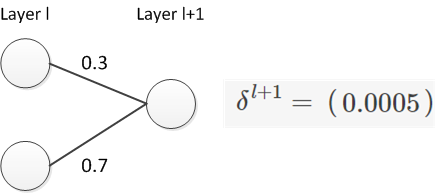
譯者注: 這里補充一個例子, 來說明為什么是反向移動了一層。
下面假設我們有一個神經網絡結構,
從上例可以看出,
然后我們把誤差反向移動后的結果與
通過合并(BP_2) 和 (BP_1) 兩個等式, 我們可以計算出任意一層的誤差量 。 我們可以先用(BP_1) 算出
等式(BP3) 是一個 以神經網絡中任意偏倚量為參照的成本函數改變速率 有關的等式:
這個等式說明, 偏差量
等式中, 誤差
等式(BP4) 是一個 以神經網絡中任意權重為參照是成本函數的改變速率 相關的等式:
這個等式告訴我們如何利用我們已經知道怎么計算的
這個等式中,
等式 (32) 有一個很好的推論是, 當**量
沿著這四大基本方程, 很有很多其他的結論。 然我們從輸出層開始, 考慮等式(BP1) 中的
當
從前面的神經元層中, 我們也可以獲得類似的見解。具體來說, 可以注意觀察一下 等式(BP2)中的
注: 之所以說有可能會變小, 是因為考慮到
總結一下, 我們從之前的分析中了解到, 無論是輸入神經元處于低**態 或是輸出神經元處于飽和態(低**態或高**態), 一個權重的學習過程都會變緩慢。
這些發現都沒什么讓人感到驚訝的地方。 他們依舊只是幫我們改善我們頭腦里神經網絡的模型, 以更好地理解神經網絡是如何學習的。 進一步, 我們可以把這類的推理進行推廣。 之前列出的四個基本等式不僅針對標準的 S型函數成立, 對任意類型的**函數也是成立的(這是因為, 等式的證明過程中沒有使用任何獨屬于 S型函數的特殊性質, 這個證明過程我們之后會看到)。 因此我們可以使用這些等式來設計一些具備我們所期待性質的**函數。 下面通過一個例子來進行說明, 假設我們選擇了一個(非S型)**函數
問題:
修改反向傳播函數的等式: 我已經使用 Hadmard 乘積的方式展示了反向傳播函數的等式(BP1 和 BP2)。 這種展示形式可能讓不熟悉 Hadmard 乘積符號的人感到不習慣。 其實還有一種使用矩陣乘法表示的方法, 一些讀者可能會對此更加熟悉。
(1) 嘗試證明 (BP1) 可以被重寫為下面的形式:
其中
- (2)嘗試證明(BP2) 可以被重寫為
δl=Σ′(zl)(wl+1)Tδl+1.(34) - (3) 把 (1)和 (2) 的結果合并證明:
對于熟悉矩陣乘法的讀者來說, 這些等式可能比 (BP1) 和 (BP2) 更容易理解。 而我專注于 (BP1) 和 (BP2) 的原因是, 這種表示方法的數學實現起來更快。
四個基礎等式的證明(選讀)
我們現在來證明四個基礎等式(BP1)- ( BP4 ). 這四個等式都是多變量微積分鏈式法則的結果。 如果你熟悉鏈式法則的話, 我強力建議你在閱讀前嘗試自行推導。
讓我們從等式(BP1) 開始, 該等式給我們提供了一個關于輸出誤差的表達式
應用鏈式法則, 我們可以將上面的偏導數重新表達為與輸出變量有關的形式。
其中, 求和函數是針對輸出層的所有神經元 k 進行的。 顯然, 當 k = j 時, 第 k 個神經元的輸出**量
回想起
這恰恰就是(BP1) 的成分表達形式。
下面我們將會證明 (BP2), 該等式為我們提供了前后兩層的誤差量
在最后一行, 我們交換了 (41) 中兩項的位置, 然后根據
進行微分以后, 我們得到:
這恰恰就是 (BP2) 的成分形式。
我們最后想要證明的等式是 (BP3) 和 (BP4) , 這些也是使用鏈式法則證明的, 和前兩個證明的方法類似。 我把后面的證明留給讀者作為一個小練習。
$$練習題
- 證明等式(BP3) 和 (BP 4)
至此就完成了反向傳播的四個基本等式的證明。 證明過程看上去好像比較復雜, 但是它確實只是應用鏈式法則的結果。 說的啰嗦一點, 我們可以把反向傳播看做是通過應用多變量微積分的鏈式法則來計算成本函數梯度的一種方式。 這真的就是反向傳播的全部了。 其余的都是細節。
反向傳播算法
反向傳播算法給我們提供了一種計算成本函數梯度的方法, 讓我們把這個過程用算法形式描述出來:
- 輸入
x :設置輸入層的**量a1 - 前向反饋 : 針對每一層
l=2,3,...,L 計算zl=wlal?1+bl 和al=σ(zl) . - 輸出誤差量
δL : 計算向量δL=?aC⊙σ′(zL) - 反向傳播誤差量: 對每一層
l=L?1,L?2,…,2 , 計算δl=((wl+1)Tδl+1)⊙σ′(zl) - 輸出: 成本函數的梯度可以通過計算
?C?wljk=al?1kδlj 和?C?blj=δlj 得到。
審視這個算法, 你會發現為什么它被稱為“反向傳播”, 我們是從最后一層開始反向計算誤差向量
練習題
單個神經元被修改過后的反向傳播:
- 假設我們在前向反饋網絡中修改單一的一個神經元, 使得該神經元的輸出為
f(∑jwjxj+b) , 其中f 是某個非 S 形函數。 這種情況下, 我們該如何修改反向傳播算法呢?
- 假設我們在前向反饋網絡中修改單一的一個神經元, 使得該神經元的輸出為
線性神經元網絡的反向傳播:
- 假設我們把非線性的
σ 函數替換為線性函數σ(z)=z , 請為這種情形重寫反向傳播算法。
- 假設我們把非線性的
正如我之前所描述的, 反向傳播算法計算針對單一的一個訓練輸入計算了成本函數的梯度,
- 輸入一個訓練抽樣的集合
- 對每一個訓練抽樣 x : 設置對應的輸入**量
ax,1 , 并且進行下面的步驟:
- 前向反饋: 針對每一層
l=2,3,...,L 計算zx,l=wlax,l?1+bl 和ax,l=σ(zx,l) . - 輸出誤差量
δx,L : 計算向量δx,L=?aC⊙σ′(zx,L) - 反向傳播誤差量: 對每一層
l=L?1,L?2,…,2 , 計算δx,l=((wl+1)Tδx,l+1)⊙σ′(zx,l)
- 前向反饋: 針對每一層
- 梯度下降: 針對每一層
l=L,L?1,…,2 , 根據規則wl→wl?ηm∑xδx,l(ax,l?1)T 和bl→bl?ηm∑xδx,l
當然, 為了實現梯度下降算法, 你還需要在上面算法的外層嵌套一個對迷你集的遍歷循環, 然后在更外層套一個游歷多訓練世代(epoch) 的循環。 為了間接, 這些循環被省略了。
反向傳播算法的代碼
在抽象地理解了反向傳播算法后, 我們現在可以理解上一章用于實現反向傳播算法的代碼了。 回想上一章節包含在 Network 類中的 update_mini_batch 和 backprop 方法。 這些代碼是上面所描述的算法的一個直譯實現。 具體而言, update_mini_batch 方法通過計算當前 mini_batch 訓練集抽樣的梯度來更新 Network 的權重和偏倚量:
class Network(object):
...
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The "mini_batch" is a list of tuples "(x, y)", and "eta"
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]大部分的工作都被該行代碼:delta_nabla_b, delta_nabla_w = self.backprop(x, y) 完成了, 該行代碼應用了 backprop 方法來算出偏導數
class Network(object):
...
def backprop(self, x, y):
"""Return a tuple "(nabla_b, nabla_w)" representing the
gradient for the cost function C_x. "nabla_b" and
"nabla_w" are layer-by-layer lists of numpy arrays, similar
to "self.biases" and "self.weights"."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# backward pass
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
...
def cost_derivative(self, output_activations, y):
"""Return the vector of partial derivatives \partial C_x /
\partial a for the output activations."""
return (output_activations-y)
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))問題
- 完全基于矩陣進行的迷你集反向傳播算法 。 我們目前的隨機梯度下降算法實現是在迷你集的訓練抽樣上進行循環完成的, 但其實我們可以通過修改反向傳播算法, 使得一個迷你集的訓練抽樣的梯度可以被同時計算出來。 方法是我們不再從一個單個輸入向量 x 開始計算, 而是從一個輸入矩陣
X=[x1x2…xm] 開始, 其中的每一列就對應著迷你集中的每一個輸入向量。 我們通過乘以權重矩陣, 然后加上一個對應的偏移量矩陣, 然后在每一個項上應用 S 形函數。 現在請你把這個方法的偽代碼寫出來。 然后修改network.py使得它用這個完全基于矩陣的方法來進行計算。 這種方法的好處是, 它可以完全利用現代的線性代數代碼實現庫, 加速對于迷你集的循環。 (在我的筆記本電腦上, 對于上一章我們所解決的 MNIST 的分類問題可以加速1/2) 。 實踐中, 所有正式的反向傳播算法庫都會使用這種完全基于矩陣的方法, 或是該方法的變種形式。
在哪種意義上, 反向傳播算法是一個快速的算法?
在哪種意義上, 反向傳播算法是一個快速的算法? 為了回答這個問題, 讓我考慮另外一種計算梯度的方法。 想象現在是神經網絡研究的早期, 可能是19世紀50-60 年代, 你是世界上第一個考慮用梯度下降方法來進行學習的人!但是為了實現這個想法, 你需要計算成本函數的梯度。 你回想了你關于微積分的只是, 然后決定嘗試看你是否能用鏈式法則來計算梯度。 但是在做了一些嘗試后, 代數等式變得復雜起來, 你有一些沮喪。 于是你試圖尋找另外一種方法。 你決定把成本當做一個僅僅有關權重的方程
其中,
這個方法看上去非常有前景。 概念上足夠簡單, 極度易于實現,僅僅幾行代碼就能實現。 當然, 這看上去比鏈式法則來計算梯度更有誘惑力!
不幸的是, 這個方法雖然好像很有前景, 但是當你用代碼實現后會發現它極度緩慢。 為了理解它為什么很慢, 想象我們的神經網絡中有一千萬哥權重。 那么針對每一個不同的權重
反向傳播的聰明之處在于, 它可以使我們僅僅用一次網絡的前向迭代計算和緊隨其后的一次反向迭代計算, 就同時計算所有的偏導數
這個加速方法是1986年第一次被完全接受, 之后極大地擴展了神經網絡可以解決的問題范圍。 這樣, 又反過來促進一大批人使用神經網絡。 當然, 反向傳播不是一個靈丹妙藥。 甚至在19世紀80年代, 人們就遭遇了該方法的瓶頸, 尤其是當人們視圖用這個方法訓練深度神經網絡(有很多隱藏層的神經網絡)時。 在這本書的后面,我們會看到現代計算機和一些聰明的想法是如何使得用反向傳播訓練深度神經網絡成為可能的。
反向傳播: 整體圖景
正如我之前解釋過的, 反向傳播算法有兩個神秘之處。
第一, 這個算法到底做了什么。 我們已經了解了誤差量從輸出被反向傳播的過程。 但是, 我們能進一步深入, 對我們所做的這一系列矩陣和向量乘法構建出更多的直覺性認識嗎?
第二, 一個人如何才能在沒有先行者參考的情況下, 發現這個算法。 理解算法的步驟, 或甚至理解算法的證明過程是一回事, 理解一個問題,然后作為第一個人獨立發現解決這個問題的算法又是另一回事。 有沒有一條可行的推理線索可以指引你發現反向傳播算法?
在這一小節, 我會解答這兩個謎題
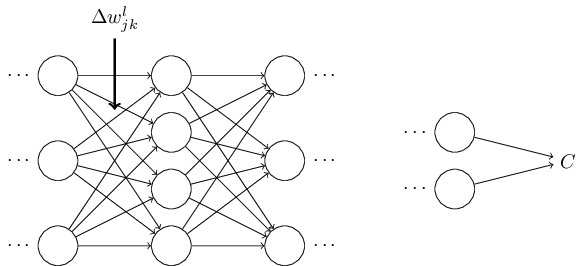
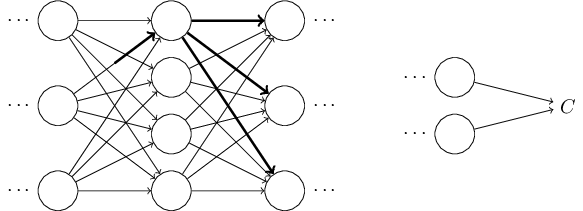
為了改善我們對反向傳播算法工作內容的直覺性理解, 讓我們想象我們對神經網絡中的某個權重
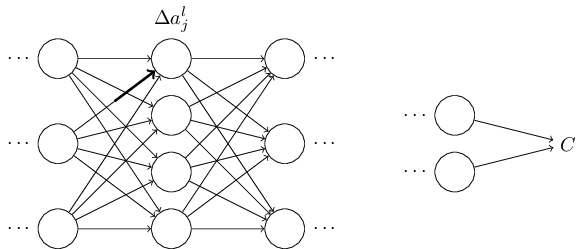
這會導致對應的神經元的**量發生改變:
然后這會進一步會導致下一層所有的神經元**量都發生變化:
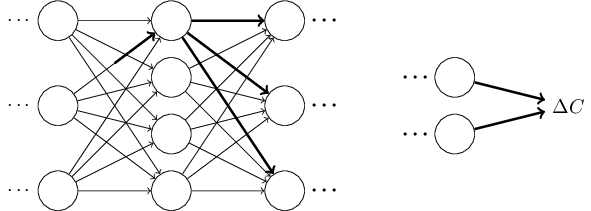
這些改變會進一步導致下一層的變化, 依次類推直到影響最后一層的輸出, 然后影響到成本函數值的變化。
成本函數值的改變量
這給我們提供了一個思路, 可以通過仔細地觀察
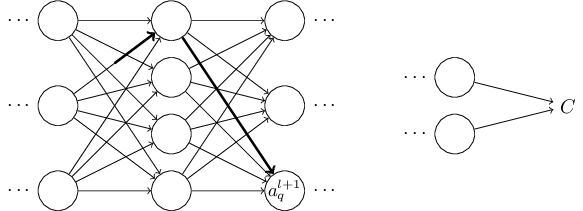
讓我們來試著實現它。 改變量
**量的改變
事實上, 它會導致如下的變化:
用等式 (48) 進行代入得到
當然, 改變量
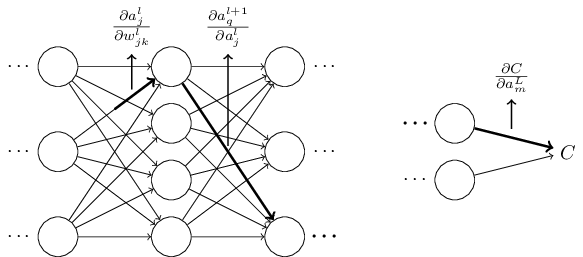
其中, 我們為每一個經過的神經元都選用了
其中, 我們加總了所有所有可能的神經元序列組合。 和公式 (47) 進行對比, 我們可以得到:
現在等式(53) 看起來比較復雜了。 然而, 它卻有一個很好的直覺性解釋。 我們在計算成本 C 相對于神經網絡中的一個權重變化率, 而這個等式告訴我們, 神經網絡中的兩個神經元之間的每一條邊(權重)都和一個因子存在某種聯系, 這個因子就是其中一個神經元的**量相對于另外一個**量的偏導數。 而連接兩個神經元的路徑上的第一條邊的因子比較特殊, 是
剛才所展示的只是一個啟發性質的論證, 一種用于思考對權重進行微調后會發生什么的方法。 現在讓我們勾勒出一條線索, 使你可以進一步深化這個論證。
首先, 你可以推到中等式(53)中每一個偏導數的表達式, 這用于一點微分學知識就能做到。 完成了之后, 你可以嘗試這思考如何把這個包含眾多下標的求和公式寫成矩陣相乘的形式。 這件事真的做起來會乏味, 還需要一些毅力, 但不需要超凡的洞察力。 在完成了所有這些后, 試著對其進行盡可能的簡化, 你會發現你最終就得到了反向傳播算法。 然后你就可以把反向傳播算法當做一個為所有路徑求因子和的方式。 或者, 換種說法, 反向傳播算法是一種追蹤權重(偏倚量)的變動如何一步步擴散至輸出, 最后影響成本的方法。
現在, 我并不打算一步步展示這個過程。 它非常散亂且需要極度的細心去完成好每個細節。 如果你有興趣挑戰一下, 你可能會享受這個嘗試的過程。 如果你不感興趣, 那么我希望這個思考過程可以為你提供一些反向傳播算法工作原理的深入認識。
現在討論另一個謎題, 反向傳播算法是如何被第一個人發現的呢?事實上, 如果你沿著我剛才所描述的方法進行嘗試, 就會發現反向傳播算法的證明方法。 不幸的是, 這個證明非常長, 且比我本章之前的描述要冗長許多。 那么, 問題就來了, 短的那個證明是如何被發現的。 事實上, 當你寫下來長的證明方式的所有細節后, 你會發現其中有好幾處非常明顯的可以簡化的地方。 你進行這些簡化, 會得到一個更短的證明。 然后把它寫下來, 你會進一步發現可以簡化的地方, 你再次重復。 在經過幾次重復操作后, 你就會得到我們先前看到的, 簡短的, 但是有一些晦澀的證明, 晦澀的原因是簡化的過程相當于去除了你一路推導的路標。 我想請你相信我,要推導出之前的證明, 真的不存在什么神秘之處, 它就是對我之前所勾勒的證明過程做了很多簡化工作而已。
智能推薦
《Neural Networks and Deep Learning》的理論知識點
目錄 目錄 深度學介紹 神經網絡基礎 淺層神經網絡 深度神經網絡 深度學介紹 AI比喻新電是是因為AI就像大約100年前的電力一樣,正在改變多個行業,如: 汽車行業,農業和供應鏈。 深度學習最近起飛的原因是:硬件的開發,特別是GPU的計算,是我們獲得更多的計算能力;深度學習已在一些重要的領域應用,如廣告,語音識別和圖像識別等等;目前數字化的時代使得我們擁有更多的數據。 關于迭代不同ML思想的圖: ...
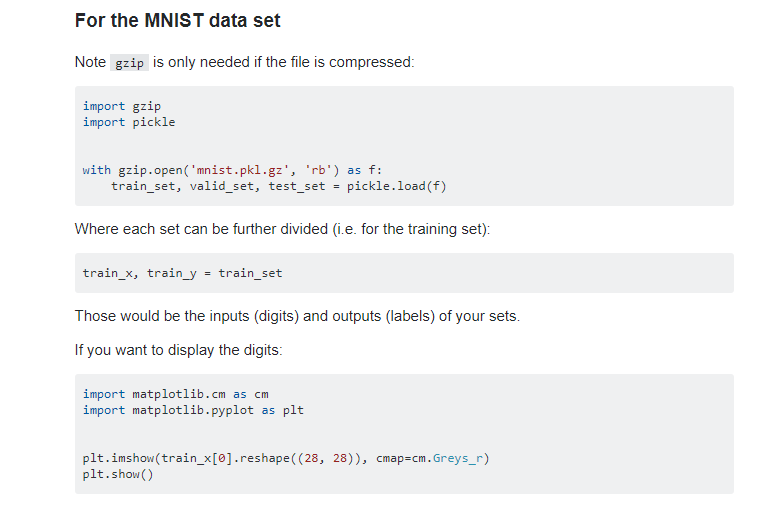
Neural Networks and Deep Learning 的MNIST數據可視化
Neural Networks and Deep Learning中我有跟著作者一直閱讀這本書,但是后來看到了第三章 可以覺得內容有點冗長,總結了一下,我自己過去一周閱讀第三章花費了不少時間,但是收獲不是很多(因為第三章的內容在第一第二章已經提過),后來甚至老師在提出希望我每十天總結一篇學習匯報的時候 我無從下手 于是我就去和別人討論自己的問題, 總結自己的問題 首先,第一第二章對于初學者來書真是...
《neural networks and deep learning》——使用神經網絡識別手寫數字
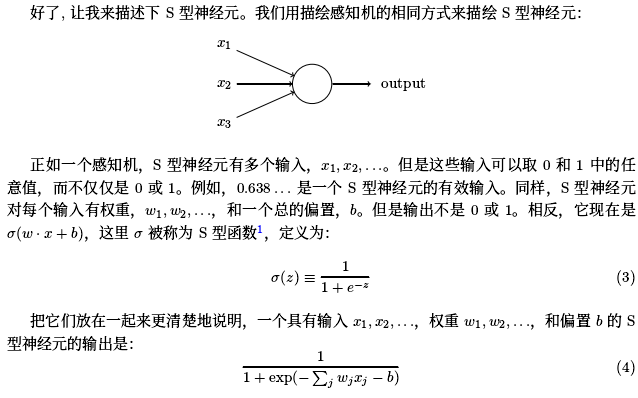
英文在線閱讀:http://neuralnetworksanddeeplearning.com/ 中文名:《神經網絡和深度學習》 中文譯文:http://download.csdn.net/download/u012123511/ 1.1 感知機 示例如下: 感知機有三個輸入,x 1 ,x 2 ,x 3 。通常可以有更多或更少輸入。Rosenblatt 提議一個簡單的規則來計算輸出。他引入權重,w...
Neural Networks and Deep Learning讀書筆記--神經網絡調參
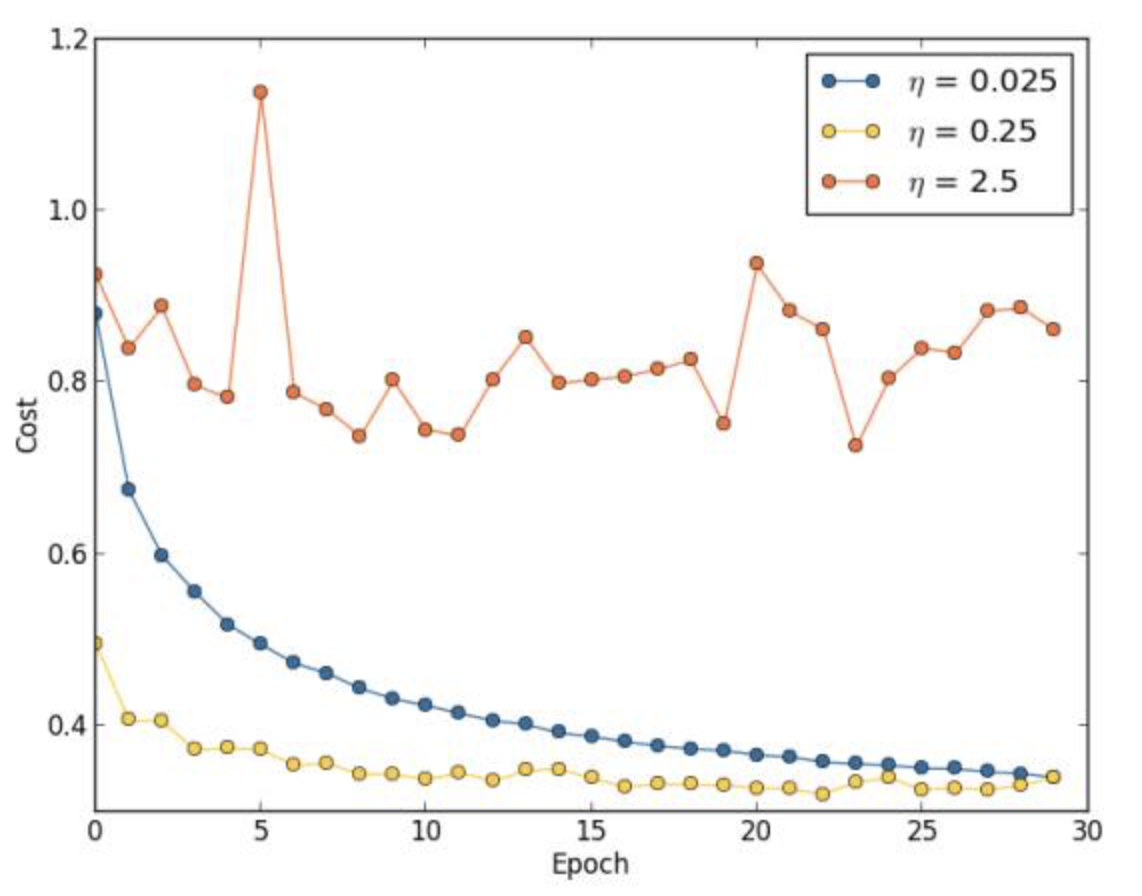
如何選擇神經網絡的超參數 在之前的實驗中我們靠運氣選擇了一些參數設置:30個隱層,小批量數據大小為10,迭代訓練30輪,使用交叉熵損失函數。但是,在使用學習速率=10.0 而規范化參數 =1000.0,我們的一個運行結果如下: 分類準確率并不比隨機選擇更好。網絡就像隨機噪聲產生器一樣。 你可能會說,“這好辦,降低學習速率和規范化參數就好了。”但是不能先驗地知道這些就是需要調...
Neural Networks and Deep Learning week2 Python Basics with numpy (optional)
該實驗作業的主要目的 熟悉使用jupyterlab來編寫python代碼 sigmoid numpy一些函數的使用 shape和reshape修改向量 python的廣播特性 向量化代碼以減少循環loop numpy的幫助文件 https://numpy.org/doc/stable/index.html 總體進程 熱身 寫一個hello world 1.1 寫一個sigmoid函數 當...
猜你喜歡
Neural Networks and Deep Learning - 神經網絡與深度學習 - Overfitting and regularization - 過擬合和正則化
Neural Networks and Deep Learning - 神經網絡與深度學習 - Overfitting and regularization - 過擬合和正則化 Neural Networks and Deep Learning http://neuralnetworksanddeeplearning.com/index.html 神經網絡與深度學習 https://legacy....
第一課:Neural Networks and Deep Learning 第二周:練習編程作業 Python Basics with numpy (optional)
第一課:Neural Networks and Deep Learning 第二周:練習編程作業Python Basics with numpy (optional) 本周課程筆記見:第二周:神經網絡的編程基礎(Basics of Neural Network programming) Python Basics with Numpy (optional assignment) Welcome t...
Neural Networks and Deep Learning(week2)神經網絡的編程基礎 (Basics of Neural Network programming)...
總結 一、處理數據 1.1 向量化(vectorization) (height, width, 3) ===> 展開shape為(heigh*width*3, m)的向量 1.2 特征歸一化(Normalization) 一般數據,使用標準化(Standardlization), z(i) = (x(i) - mean) / delta,mean與delta代表X的均值和標準差,最終特征處...
freemarker + ItextRender 根據模板生成PDF文件
1. 制作模板 2. 獲取模板,并將所獲取的數據加載生成html文件 2. 生成PDF文件 其中由兩個地方需要注意,都是關于獲取文件路徑的問題,由于項目部署的時候是打包成jar包形式,所以在開發過程中時直接安照傳統的獲取方法沒有一點文件,但是當打包后部署,總是出錯。于是參考網上文章,先將文件讀出來到項目的臨時目錄下,然后再按正常方式加載該臨時文件; 還有一個問題至今沒有解決,就是關于生成PDF文件...