Tensorflow 實戰 Google 深度學習框架 | 學習筆記(二)
標簽: Tensorflow 神經網絡 損失函數
Shoot on the moon and if you miss you will still be among the stars.
Caicloud Github :tensorflow-tutorialhttps://github.com/caicloud/tensorflow-tutorial
原 tutorial 使用的 Tensorflow 最新版本是 1.4.0 ,本人使用的 1.5.0 版本,所以部分代碼會略有不同,該筆記僅為個人學習,理解使用。如有錯誤,還望批評指教。—-ZJ
4 深層神經網絡
4.1 深度學習與深層神經網絡
wiki 深度學習定義:一類通過多層非線性變換對高復雜性數據建模算法的合集。
深度學習,兩個重要特性:多層 and 非線性。
線性模型的局限性,線性模型能夠解決的問題是有限的(解決線性可分的問題)。
- 3.4.2 小節中,輸出為所有輸入的加權和,導致整個神經網絡是一個線性模型。
- (采用線性函數)任意層的全連接神經網絡(FC)和單層神經網絡模型的表達能力沒有任何區別。
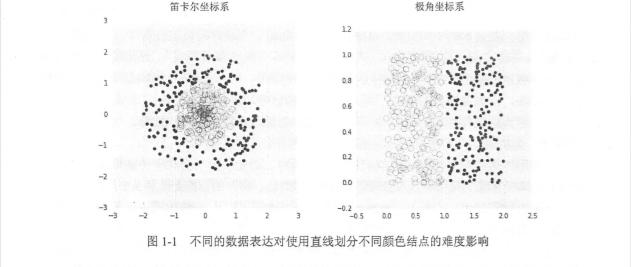
- 線性模型可以解決線性可分的問題,如通過直線(或高維空間的平面)劃分。
- 現實世界中,絕大多數問題是無法線性分割的,所以出現 Relu 這樣非線性的**函數,來解決高復雜性的問題(深度學習的目的就是解決這樣的問題)
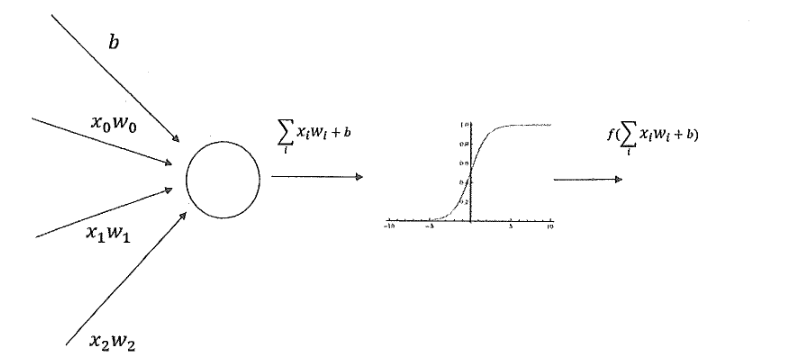
**函數實現去線性化
- 如果每個神經元的輸出通過一個非線性函數,那么整個神經網絡就不再是線性的了。
- 添加偏置項(bias),偏置項 是神經網絡中非常有用的一種結構。
- 每個節點(神經元)的輸出在 加權和的基礎上,還做了一個非線性變換。
- 常用非線性**函數(tf.nn.relu, tf.sigmoid, tf.tanh)
多層網絡解決異或運算
- 在神經網絡的發展史,有個很重要的問題,異或問題。
- 1958 感知機模型,將輸入進行加權和,沒有隱藏層,然后經過**函數最后得到輸出。不能解決異或問題。
- 異或問題(直觀理解):兩個輸入的符號相同時(同正,同負)輸出為 0 ,否則(一正一負)輸出為 1.
- 加入隱藏層后,異或問題得到很好的解決
- 深層網絡有組合特征提取的功能,這個特性對于解決不易提取特征向量的問題(如圖片識別,語音識別等)有很大的幫助。
4.2 損失函數的定義
神經網絡模型的效果以及優化的目標是通過損失函數(loss function)來定義的。
監督學習的兩大種類:分類問題 and 回歸問題。
經典損失函數
自定義損失函數
如何判斷一個輸出向量和期望的向量有多接近?——交叉熵(cross entropy)是最常用的評判方法之一。
交叉熵 (cross entropy):
給定兩個概率分布 p,q
注意:交叉熵刻畫的是兩個概率之間的分布,但是神經網絡的輸出不一定是一個概率分布。
- 概率分布刻畫了不同事件發生的概率,當事件總數有限的情況下,概率分布函數 滿足:
- 任意事件發生的概率都在 0 和 1 之間
- 且總有某一個事件發生(概率的和為 1)
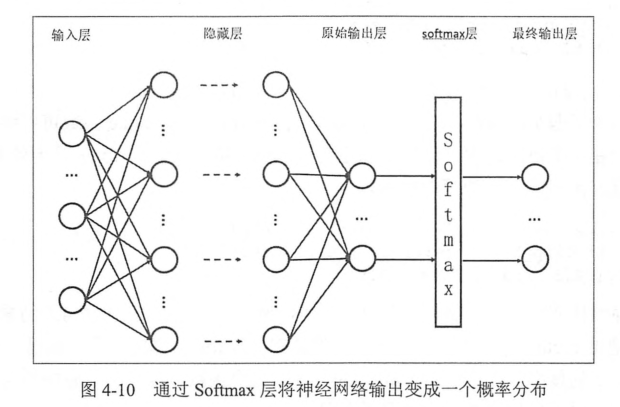
如何將神經網絡前向傳播的結果變成概率分布?
- softmax 回歸是一個常用的方法
假設原始的神經網絡輸出為 ,那么經過 softmax 處理之后的輸出為:
- 原始神經網絡的輸出被用作置信度來生成新的輸出,新的輸出滿足概率分布的所有要求
- 新的輸出可以理解為經過神經網絡的推導,一個樣本為不同類別的概率分別有多大
- 因此神經網絡的輸出變為了一個概率分布,從而可以通過交叉熵來計算預測概率分布和真實答案的概率分布之間的距離。
- 交叉熵函數不是對稱的 (),刻畫的是通過概率 q 來表達概率分布 p 的困難程度
- 在神經網絡中,p 代表正確標簽,q 代表預測值
import tensorflow as tf
tf.__version__'1.5.0'
'''
Tensorflow 實現交叉熵
'''
cross_entropy = -tf.reduce_mean(y_* tf.log(tf.clip_by_value(y, 1e-10, 1.0)))
reduce_mean 可以理解為 ,n 代表一個 batch 中樣例的數量
其中:y_代表正確結果, y 代表預測值
上面一行代碼,包含了 4 種不同的 Tensorflow 運算。
tf.clip_by_value函數可以將在一個張量中的數值限制在一個范圍之內,可以避免一些運算錯誤,(如 log0 是無效的)- 小于 2.5 的數值替換為 2.5 ,大于 4.5 的數值 替換為 4.5
- 通過
tf.clip_by_value函數可以保證在進行 log 運算時,不會出現 log0 這樣的錯誤
import tensorflow as tf
v = tf.constant([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
with tf.Session() as sess:
print(tf.clip_by_value(v, 2.5, 4.5).eval())
[[2.5 2.5 3. ]
[4. 4.5 4.5]]
- 第二個運算是
tf.log函數,完成對張量中所有函數一次求對數的功能
v = tf.constant([1.0, 2.0, 3.0])
with tf.Session() as sess:
print(tf.log(v).eval())[0. 0.6931472 1.0986123]
- 第三個是乘法運算,在實現交叉熵的代碼中直接將兩個矩陣通過
*操作相乘,這個操作不是矩陣乘法,而是元素之間直接相乘 (element-wise) - 矩陣乘法需要使用
tf.matmul函數完成。下面示例給出兩者區別:
v1 = tf.constant([[1.0, 2.0], [3.0, 4.0]])
v2 = tf.constant([[5.0, 6.0], [7.0, 8.0]])
with tf.Session() as sess:
print('逐元乘積:\n',(v1*v2).eval())
print('矩陣乘法:\n', tf.matmul(v1, v2).eval())逐元乘積:
[[ 5. 12.]
[21. 32.]]
矩陣乘法:
[[19. 22.]
[43. 50.]]
v1 * v2的結果是每個位置上對應元素的乘積,如結果中(1,1)元素值 5 是1×5 = 5tf.matmul函數完成矩陣乘法 ,如 (1,1)元素值 19 是1× 5 + 2× 7 = 19上面三個運算完成了對每一個樣例中每個類別交叉熵
p(x)logq(x)的計算- 這三步計算分別得到的結果是一個
n × m的二維矩陣,n 為一個 batch 中樣例的數量, m 為分類的類別數量。 - 根據該交叉熵的公式,應該將每行中的 m 個結果相加得到所有樣例的交叉熵
- 然后再對這 n 行取平均得到一個 batch 的平均交叉熵
- 因為分類問題的類別數量是不變的,所以可以直接對整個矩陣做平均而不改變計算結果的意義
- 簡單展示
tf.reduce_mean函數的使用方法
v = tf.constant([[1.0,2.0,3.0],[4.0,5.0,6.0]])
with tf.Session() as sess:
print(tf.reduce_mean(v).eval())3.5
- 因為 交叉熵一般會和 softmax 回歸一起使用,所以 Tensorflow 對這兩個功能進行了統一封裝 ,并提供
tf.nn.softmax_cross_entopy_with_logits函數 - 可以通過下面代碼來實現使用了 softmax 回歸之后的交叉熵損失函數
# y 是預測輸出值,y_ 是標準答案
cross_entopy = tf.nn.softmax_cross_entropy_with_logits(y,y_)
- 回歸問題解決的是對具體數值的預測,如房價預測,銷量預測等。
- 解決回歸問題的神經網絡一般只有一個輸出節點,輸出值為預測值。
- 回歸問題最常用的是損失函數是均方誤差(MES, mean squared error)
- 為一個 batch 中第 i 個數據的正確答案, 為神經網絡給出的預測值
- Tensorflow 實現均方誤差損失函數
mse = tf.reduce_mean(tf.square(y_ - y))
其中:y_代表標準答案, y 代表神經網絡輸出值
4.2.2 自定義損失函數
- Tensorflow 支持任意優化的自定義損失函數
- 下面公式給出一個 當預測多于真實值和預測少于真實值時有不同系數的損失函數
- 為一個 batch 中第 i 個數據的正確答案, 為神經網絡給出的預測值 a,b 是常量,如 a = 10 , b = 1,TF 實現:
loss = tf.reduce_sum(tf.where(tf.greater(v1,v2),(v1 - v2) * a, (v2- v1) *b ))- 用到了
tf.greater和tf.where來實現選擇操作 tf.greater的輸入是兩個張量,此函數會比較這兩個輸入張量中每一個元素的大小,并返回比較結果- 當
tf.greater的輸入張量維度不一樣是,TF 會進行類似 Numpy 廣播(broadcasting) 的處理。 tf.where有三個參數,1.選擇條件根據,當選擇條件 為 True 時,tf.where函數會選擇第二個參數中的值,否則使用第三個參數中的值。- 注意:
tf.where函數判斷和選擇都是在元素級別進行,下面展示用法:
v1 = tf.constant([1.0, 2.0, 3.0, 4.0])
v2 = tf.constant([4.0, 3.0, 2.0, 1.0])
sess = tf.InteractiveSession()
print(tf.greater(v1, v2).eval())
print(tf.where(tf.greater(v1,v2),v1,v2).eval())
sess.close()[False False True True]
[4. 3. 3. 4.]
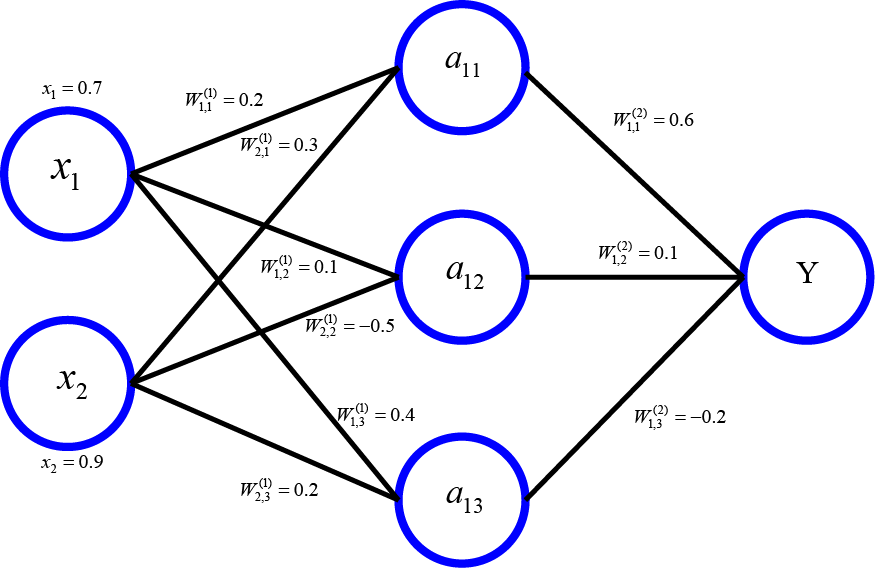
下面通過一個簡單的神經網絡程序來講解損失函數對模型訓練結果的影響。
- 兩個輸入節點,一個輸出節點,沒有隱藏層
import tensorflow as tf
from numpy.random import RandomState
'''
1. 定義神經網絡的相關參數和變量。
'''
batch_size = 8
# 輸入兩個節點
x = tf.placeholder(tf.float32, shape=(None, 2), name='x-input')
# 回歸問題一般只有一個輸出節點
y_ = tf.placeholder(tf.float32, shape=(None, 1), name='y-input')
# 定義一個單層神經網絡的前向傳播過程,這里是簡單加權和 stddev=1 標準差
w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)
'''
2. 設置自定義的損失函數。
'''
# 定義預測多了和預測少了的 成本
loss_less = 10 # 預測少了 會損失 10塊
loss_more = 1 # 預測多了 只損失 1 塊
loss = tf.reduce_sum(tf.where(tf.greater(y,y_),
(y - y_) * loss_more,
(y_ - y) * loss_less))
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
'''
3. 生成模擬數據集。
'''
# 通過隨機數生成一個數據模擬集 128 個樣本,每個樣本兩個特征
rdm = RandomState(1)
X = rdm.rand(128, 2)
print(X.shape)
# print(X)
'''
設置回歸的正確值為兩個輸入的和加上一個隨機量,之所以要加上一個隨機量是為了
加入不可預測的噪音,否則不同損失函數的意義就不大了,因為不同損失函數都會在能
完全預測正確的時候最低,一般來說噪音是一個均值為 0 的小量,所以這里的
噪音設置為 -0.05 ~ 0.05 的隨機數
'''
# Y 正確值 是一個 list (x1, x2) in X 一個樣本有兩個特征,128 行 2 列
Y = [[x1 + x2 + (rdm.rand()/10.0-0.05)] for (x1, x2) in X]
'''
4.訓練模型。
'''
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 5000
for i in range(STEPS):
start = (i*batch_size) % 128
end = (i*batch_size) % 128 + batch_size
sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
if i % 1000 == 0:
print("After %d training step(s), w1 is: " % (i))
print(sess.run(w1), "\n")
print("Final w1 is: \n", sess.run(w1)) (128, 2)
After 0 training step(s), w1 is:
[[-0.81031823]
[ 1.4855988 ]]
After 1000 training step(s), w1 is:
[[0.01247112]
[2.1385448 ]]
After 2000 training step(s), w1 is:
[[0.45567414]
[2.1706066 ]]
After 3000 training step(s), w1 is:
[[0.69968724]
[1.8465308 ]]
After 4000 training step(s), w1 is:
[[0.89886665]
[1.2973602 ]]
Final w1 is:
[[1.019347 ]
[1.0428089]]
'''
5. 重新定義損失函數,使得預測多了的損失大,于是模型應該偏向少的方向預測。
'''
loss_less = 1
loss_more = 10 # 預測多了的損失大
loss = tf.reduce_sum(tf.where(tf.greater(y, y_),(y - y_)* loss_more, (y_ - y) * loss_less))
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
STEPS = 5000
for i in range(STEPS):
start = (i*batch_size) % 128
end = (i*batch_size) % 128 + batch_size
sess.run(train_step, feed_dict={x:X[start:end], y_:Y[start:end]})
if i % 1000 == 0:
print("After %d training step(s), w1 is: " % (i))
print(sess.run(w1), "\n")
print("Final w1 is: \n", sess.run(w1))
After 0 training step(s), w1 is:
[[-0.8123182]
[ 1.4835987]]
Final w1 is:
[[-0.8123182]
[ 1.4835987]]
Final w1 is:
[[-0.81303465]
[ 1.4826417 ]]
Final w1 is:
[[-0.81253535]
[ 1.4817047 ]]
......
Final w1 is:
[[0.95506585]
[0.98148215]]
Final w1 is:
[[0.9552581]
[0.9813394]]
'''
6. 定義損失函數為MSE。
'''
loss = tf.losses.mean_squared_error(y,y_)
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
STEPS = 5000
for i in range(STEPS):
start = (i*batch_size) % 128
end = (i*batch_size) % 128 + batch_size
sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
if i % 1000 == 0:
print("After %d training step(s), w1 is: " % (i))
print(sess.run(w1), "\n")
print("Final w1 is: \n", sess.run(w1))
After 0 training step(s), w1 is:
[[-0.81031823]
[ 1.4855988 ]]
Final w1 is:
[[-0.81031823]
[ 1.4855988 ]]
……
Final w1 is:
[[0.9741856]
[1.0243824]]
Final w1 is:
[[0.9742431]
[1.024378 ]]
Final w1 is:
[[0.9742944]
[1.0243853]]
Final w1 is:
[[0.97434247]
[1.0243782 ]]
Final w1 is:
[[0.9743756]
[1.0243336]]
- 第一種得到的 w1= [[1.019347 ],[1.0428089]],也就是得到的預測函數 比 大,因為在損失函數中,規定的是 預測少了損失更大,所以為了降低損失,預測值會更大些
- 第二種,將 loss_more 和 loss_less 調整后,w1 = [[0.9552581],[0.9813394]] ,預測多了損失更大,所以,少預測一些會降低損失
- 第三種,使用 MSE 均方誤差作為損失函數 [[0.9743756],[1.0243336]] ,離標準答案更近
智能推薦
《TensorFlow:實戰Google深度學習框架(第二版)》筆記【7-12章】
第七章 圖像數據處理 本章介紹如何對圖像進行預處理使得模型盡可能不被無關因素(亮度、對比度等)所影響,同時使用多線程處理提高效率。 TFRecord輸入數據格式 tf提供了一種統一的格式存儲數據,TFRecord。第六章中花朵分類使用了字典存儲數據,這種方式擴展性很差。TFRecord可以有效地記錄來源更加復雜、信息更加豐富的數據。 TFRecord的數據都是通過tf.train.Example ...
《TensorFlow:實戰Google深度學習框架(第二版)》筆記【1-6章】
本書PDF 密碼: uj6t 代碼:https://github.com/caicloud/tensorflow-tutorial 第一章:深度學習簡介 在大部分情況下,在訓練數據達到一定數量之前,越多的訓練數據可以使邏輯回歸算法對未知郵件做出的判斷越精準。之所以說在大部分情況下,是因為邏輯回歸算法的效果除了依賴于訓練數據,也依賴于從數據中提取的特征。假設從郵件中抽取的特征只有郵件發送的時間,那么...
Tensorflow 實戰Google深度學習框架——學習筆記(三)TensorFlow中提供的網絡優化函數
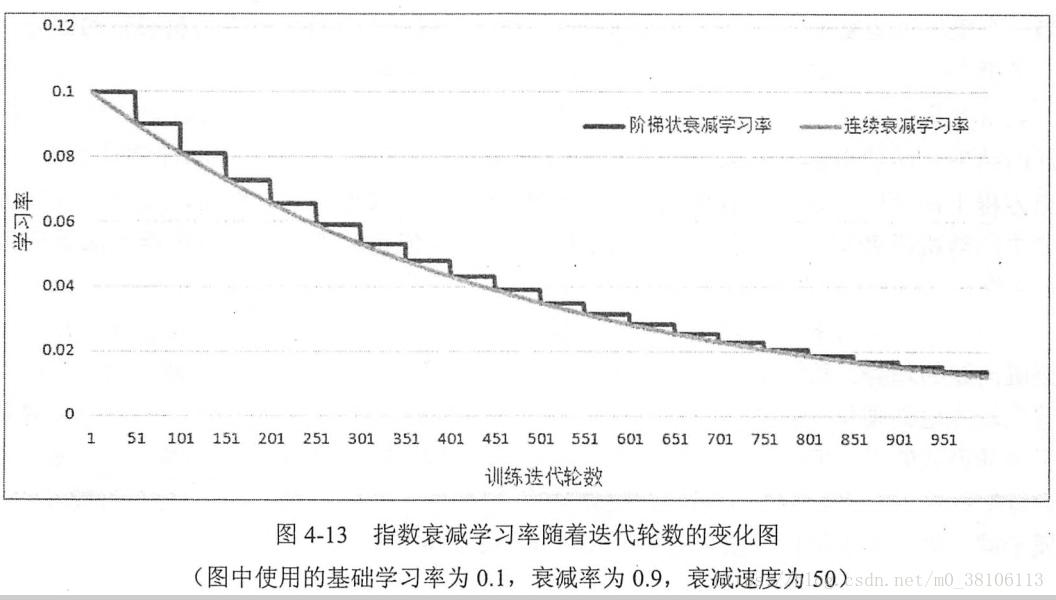
4.4.1 學習率的設置 學習率過大會導致參數在靠近最優值的時候來回擺動,過小會導致參數迭代速度太慢,TensorFlow針對這種問題提供了一種更加靈活的學習率設置方法——指數衰減法。 指數衰減法先用較大的學習率來獲得較優解,隨著迭代逐步減小學習率,使得模型在后期更加穩定地接近最優解。這個方法即是tf.tarin.exponential_decay(),它實現了以下代碼的功...
《TensorFlow-實戰Google深度學習框架》學習筆記 計算圖、張量、會話
3.1 TensorFlow計算模型——計算圖 Tensor:是張量,可以簡單理解為多維數組,相當于表明了數據結構 Flow:是流,表達張量之間通過計算相互轉化的過程...
【TensorFlow實戰Google深度學習框架】學習筆記(圖像識別與卷積神經網絡)
1、圖像識別經典數據集Cifar cifar是32x32x3的彩色圖片集 2、卷積神經網絡簡介 3、卷積神經網絡常用的結構 3.1卷積層 Filter的深度就是Filter的個數 3.2池化層 4、經典卷積神經網絡模型 卷積神經網絡結構的問題 卷積層和池化層的參數配置問題 5、卷積網絡的遷移學習 遷移學習可以總結為在別人成功的模型(網絡結構和訓練好的參數)的基礎上修改、增減自己的網絡結構。這樣做的...
猜你喜歡
TensorFlow:實戰Google深度學習框架第二版——第五章
目錄 第五章——MNIST數字識別問題 5.1 MNIST數據處理 5.2 神經網絡模型訓練及不同模型結果對比 5.2.1 TensorFlow訓練神經網絡——完整程序 5.2.2使用驗證數據集判斷模型效果 5.2.3不同模型效果的比較 5.3 變量管理 5.4 TensorFlow模型持久化 5.4.1持久化代碼實現 5.4.2 持久化原理及數據格...
04.深層神經網絡------《Tensorflow實戰Google深度學習框架》筆記
一、深度學習與深層神經網絡 維基百科對深度學習的定義:一類通過多層非線性變換對高復雜性數據建模算法的合集。又由于深層神經網絡是實現“多層非線性變換”最常用的一種方法,所以在實際中基本上可以認為深度學習就是深層神經網絡的代名詞。深度學習有兩個非常重要的特性-----多層和非線性。 1、線性模型的局限性 在線性模型中,模型...
08.循環神經網絡------《Tensorflow實戰Google深度學習框架》筆記
循環神經網絡簡介 循環神經網絡的主要用途是處理和預測序列數據。在之前介紹的全連接神經網絡或卷積神經網絡模型中,網絡結構都是從輸入層到隱含層再到輸出層,層與層之間是全連接或部分連接的,但每層之間的節點是無連接的。考慮這樣一個問題,如果要預測句子的下一個單詞是什么,一般需要用到當前單詞以及前面的單詞,因為句子中前后單詞并不是獨立的。比如,當前單詞是“很”,前一個單詞是&ldqu...
07.圖像數據處理------《Tensorflow實戰Google深度學習框架》筆記
轉自:https://blog.csdn.net/Koala_Tree/article/details/78021375 一、TFRecord輸入數據格式 TensorFlow讀取數據,總共有三種方法: 供給數據(Feeding):在TensorFlow程序運行的過程中,使用Python代碼來供給數據; 從文件讀取數據:在TensorFlow圖的起始,讓一個輸入管線從文件中讀取數據; 預加載數據:...