高斯消元學習筆記&模板&任務
模板:
#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<string.h>
#include<math.h>
using namespace std;
const int MAXN=50;
int a[MAXN][MAXN];//增廣矩陣
int x[MAXN];//解集
bool free_x[MAXN];//標記是否是不確定的變元
/*
void Debug(int equ,int var)//調試用
{
int i, j;
for (i = 0; i < equ; i++)
{
for (j = 0; j < var + 1; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
*/
inline int gcd(int a,int b)
{
int t;
while(b!=0)
{
t=b;
b=a%b;
a=t;
}
return a;
}
inline int lcm(int a,int b)
{
return a/gcd(a,b)*b;//先除后乘防溢出
}
// 高斯消元法解方程組(Gauss-Jordan elimination).(-2表示有浮點數解,但無整數解,
//-1表示無解,0表示唯一解,大于0表示無窮解,并返回自由變元的個數)
//有equ個方程,var個變元。增廣矩陣行數為equ,分別為0到equ-1,列數為var+1,分別為0到var.
int Gauss(int equ,int var)
{
int i,j,k;
int max_r;// 當前這列絕對值最大的行.
int col;//當前處理的列
int ta,tb;
int LCM;
int temp;
int free_x_num;
int free_index;
for(int i=0;i<=var;i++)
{
x[i]=0;
free_x[i]=true;
}
//轉換為階梯陣.
col=0; // 當前處理的列
for(k = 0;k < equ && col < var;k++,col++)
{// 枚舉當前處理的行.
// 找到該col列元素絕對值最大的那行與第k行交換.(為了在除法時減小誤差)
max_r=k;
for(i=k+1;i<equ;i++)
{
if(abs(a[i][col])>abs(a[max_r][col])) max_r=i;
}
if(max_r!=k)
{// 與第k行交換.
for(j=k;j<var+1;j++) swap(a[k][j],a[max_r][j]);
}
if(a[k][col]==0)
{// 第k行col列是最大值了,此時為0,說明該col列第k行以下全是0了,則處理當前行的下一列.
k--;//退出循環時,k的值就能指向最后一行的行坐標了
continue;
}
for(i=k+1;i<equ;i++)
{// 枚舉要刪去的行.
if(a[i][col]!=0)
{
LCM = lcm(abs(a[i][col]),abs(a[k][col]));
ta = LCM/abs(a[i][col]);
tb = LCM/abs(a[k][col]);
printf("%d %d\n",ta,tb);
if(a[i][col]*a[k][col]<0)tb=-tb;//異號的情況是相加
for(j=col;j<var+1;j++)
{
a[i][j] = a[i][j]*ta-a[k][j]*tb;
}
}
}
//Debug(equ,var);
}
for(i=0;i<equ;i++){
for(j=0;j<var+1;j++)printf("%d ",a[i][j]);
printf("\n");
}
// Debug();
//printf("%d %d",k,col) ;
// 1. 無解的情況: 化簡的增廣陣中存在(0, 0, ..., a)這樣的行(a != 0).
for (i = k; i < equ; i++)
{ // 對于無窮解來說,如果要判斷哪些是自由變元,那么初等行變換中的交換就會影響,則要記錄交換.
if (a[i][col] != 0) return -1;
}
// 2. 無窮解的情況: 在var * (var + 1)的增廣陣中出現(0, 0, ..., 0)這樣的行,即說明沒有形成嚴格的上三角陣.
// 且出現的行數即為自由變元的個數.
if (k < var)
{
// 首先,自由變元有var - k個,即不確定的變元至少有var - k個.
for (i = k - 1; i >= 0; i--)//往前一行一行的方程判斷,是否存在不確定的變元,有時不確定的變元不一定是在最后一行。由k的值,倒著往前枚舉,就可以確定變元的個數了。
{
// 第i行一定不會是(0, 0, ..., 0)的情況,因為這樣的行是在第k行到第equ行.
// 同樣,第i行一定不會是(0, 0, ..., a), a != 0的情況,這樣的無解的.
free_x_num = 0; // 用于判斷該行中的不確定的變元的個數,如果超過1個,則無法求解,它們仍然為不確定的變元.
for (j = 0; j < var; j++)
{
if (a[i][j] != 0 && free_x[j]) free_x_num++, free_index = j;
}
if (free_x_num > 1) continue; // 無法求解出確定的變元.
// 說明就只有一個不確定的變元free_index,那么可以求解出該變元,且該變元是確定的.
temp = a[i][var];
for (j = 0; j < var; j++)
{
if (a[i][j] != 0 && j != free_index) temp -= a[i][j] * x[j];
}
x[free_index] = temp / a[i][free_index]; // 求出該變元.
free_x[free_index] = 0; // 該變元是確定的.
}
return var - k; // 自由變元有var - k個.
}
// 3. 唯一解的情況: 在var * (var + 1)的增廣陣中形成嚴格的上三角陣.
// 計算出Xn-1, Xn-2 ... X0.
for (i = var - 1; i >= 0; i--)
{
temp = a[i][var];
for (j = i + 1; j < var; j++)
{
if (a[i][j] != 0) temp -= a[i][j] * x[j];
}
if (temp % a[i][i] != 0) return -2; // 說明有浮點數解,但無整數解.
x[i] = temp / a[i][i];
}
return 0;
}
int main(void)
{
//freopen("in.txt", "r", stdin);
//freopen("out.txt","w",stdout);
int i, j;
int equ,var;
while (scanf("%d %d", &equ, &var) != EOF)
{
memset(a, 0, sizeof(a));
for (i = 0; i < equ; i++)
{
for (j = 0; j < var + 1; j++)
{
scanf("%d", &a[i][j]);
}
}
// Debug();
int free_num = Gauss(equ,var);
if (free_num == -1) printf("無解!\n");
else if (free_num == -2) printf("有浮點數解,無整數解!\n");
else if (free_num > 0)
{
printf("無窮多解! 自由變元個數為%d\n", free_num);
for (i = 0; i < var; i++)
{
if (free_x[i]) printf("x%d 是不確定的\n", i + 1);
else printf("x%d: %d\n", i + 1, x[i]);
}
}
else
{
for (i = 0; i < var; i++)
{
printf("x%d: %d\n", i + 1, x[i]);
}
}
printf("\n");
}
return 0;
}任務:
POJ 1222EXTENDED LIGHTS OUT
POJ 1681 Painter's Problem
POJ 1753 Flip Game
POJ 1830 開關問題
POJ 3185 The Water Bowls
POJ 2947 Widget Factory
POJ 1166 The Clocks
POJ 2065 SETI
POJ 1487 Single-Player Games
hdu OJ 2449
fze OJ 1704 http://acm.fzu.edu.cn/problem.php?pid=1704
HDU 4818 RP problem (高斯消元, 2013年長春區域賽F題)
HDU 3976 Electricresistance (高斯消元法)
HDU 3949 XOR(xor高斯消元)智能推薦
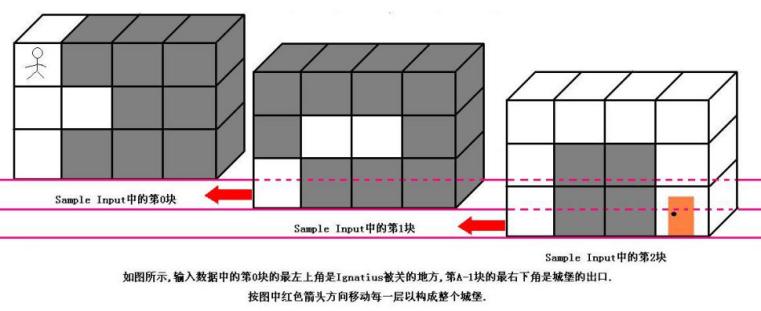
DFS&amp;BFS總結
DFS&BFS總結 目錄..........................................................................................1 B - LakeCounting.............................1 C - Red and Black...............................
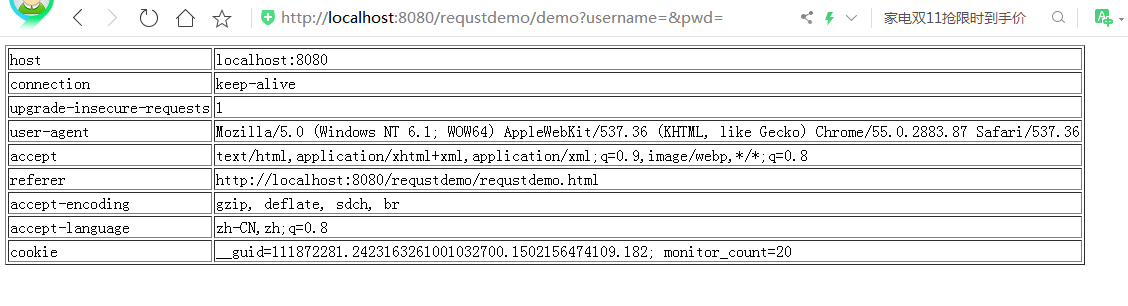
HttpServletRequest&amp;&amp;HttpServletResponse參數的接收和響應
一、請求頭信息: 二、獲取前臺傳值: 1、表單的action請求(id用于js,class用于css,name用于后臺): (1、)req.getParameter(arg)方法,參數為name值。例: (2、)req.getParameterNames()獲取所有的name值,然后再利用上面(1、)中的方法獲取value值。例: (3、)req.getParameterValues(arg);用...
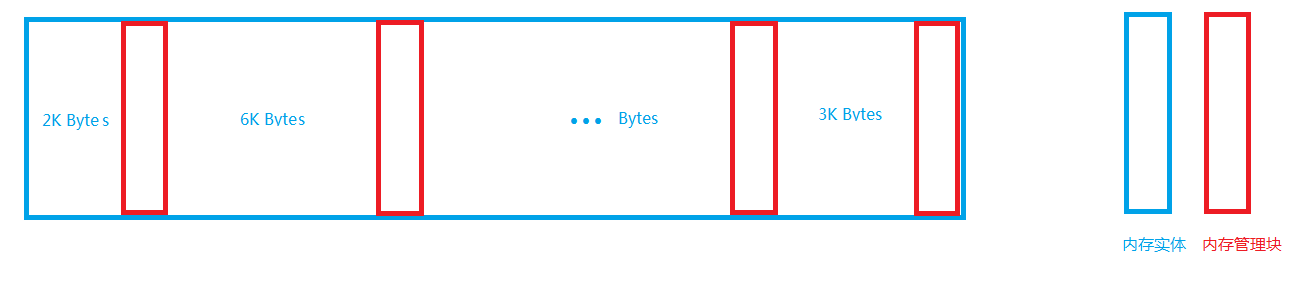
單片機上內存管理(重定義malloc &amp;amp;amp; free)de實現
在單片機上經常會需要用到像標準c庫中的內存分配,可是單片機并沒有內存管理機制,如果直接調用庫函數(malloc,free...),會導致內存碎片越用越多,很容易使系統崩潰掉,這里分享一個自己寫的適用于單片機的內存分配方法,具備輕量級的內存管理能力,有效減少內存碎片,提高單片機系統工作穩定性。 如下圖,heap_start開始的地方,是我們存放用戶...
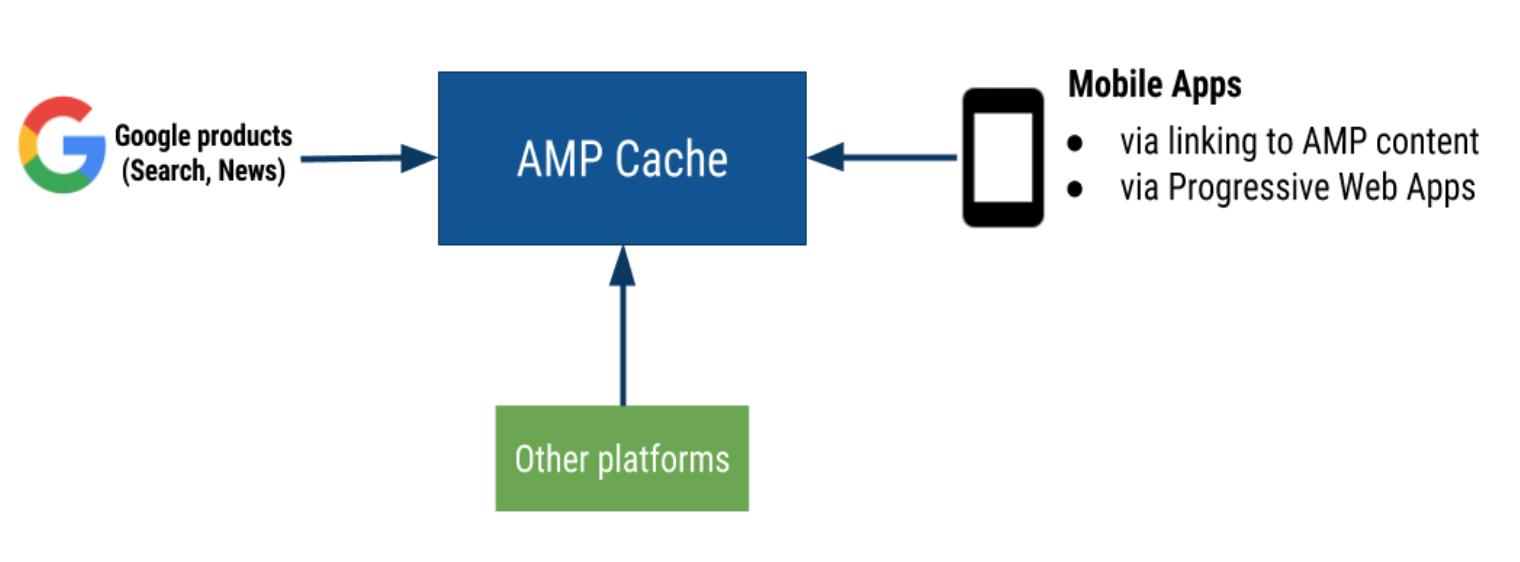
Google AMP 知識分享
AMP 是什么 AMP,全稱是 Accelerated Mobile Pages, 是 Google 推出的開源前端框架。AMP 最明顯的特征就是 性能,被稱為目前 WEB 屆最快的框架毫不夸張。 Google 對 AMP 的性能進行了極致的優化,比如 JS 和網頁數據放在緩存( 具體可看這篇文章:AMP 如何提升性能)。 是否有必要做 AMP 當然有必要做了。理由有 2 個:首先,是快...
猜你喜歡
Java中byte轉int類型為什么要&amp;amp;amp;amp;0xFF?
今天查看代碼,翻到MD5加密代碼,如下: 為什么要&0xFF ? 各種查資料,了解到,計算機中存儲都是利用二進制的補碼存儲的,存儲數據機制:正數存儲的二進制原碼,負數存儲的是二進制的補碼。 補碼是負數的絕對值反碼加1。 計算機為什么用補碼存儲數據,當我們明白這個問題后,就可以去理解另一個衍生問題——數據溢出。 首先我們看一段數據溢出的Jav...
[2018.04.17][水][日志][8][#207][計算表達式的值][calculate][-&amp;amp;amp;amp;amp;gt;][棧][代碼智熄]
[背景] 近日VHOS再次把第二頁的題目刷完了,小小慶祝一下~ 然后,當我發現線性表只有一道題被我AC時,我驚奇發現,我來到了棧的世界~ [題干][#207 計算表達式的值] 題目描述 小明在你的幫助下,破譯了Ferrari設的密碼門,正要往前走,突然又出現了一個密碼門。 門上有一個算式,其中只有“(”、“)&rdquo...
UE4新手命令教程 (后續更新)&amp;amp;amp;amp;amp;不常用但好用的藍圖節點
改變顯示模式: 改變游戲播放速度: Slomo X 分析CPU和內存 MemReport-full stat startfile stat stopfile (用虛幻自帶的SessionFrontend加載Profiler文件進行分析) 讓角色在靜態物體陰影處不暗 r.Shadow.ForceSingleSampleShadowingFromStationar...
freemarker + ItextRender 根據模板生成PDF文件
1. 制作模板 2. 獲取模板,并將所獲取的數據加載生成html文件 2. 生成PDF文件 其中由兩個地方需要注意,都是關于獲取文件路徑的問題,由于項目部署的時候是打包成jar包形式,所以在開發過程中時直接安照傳統的獲取方法沒有一點文件,但是當打包后部署,總是出錯。于是參考網上文章,先將文件讀出來到項目的臨時目錄下,然后再按正常方式加載該臨時文件; 還有一個問題至今沒有解決,就是關于生成PDF文件...