Coursera | Andrew Ng (01-week-2-2.11)—向量化
該系列僅在原課程基礎上部分知識點添加個人學習筆記,或相關推導補充等。如有錯誤,還請批評指教。在學習了 Andrew Ng 課程的基礎上,為了更方便的查閱復習,將其整理成文字。因本人一直在學習英語,所以該系列以英文為主,同時也建議讀者以英文為主,中文輔助,以便后期進階時,為學習相關領域的學術論文做鋪墊。- ZJ
轉載請注明作者和出處:ZJ 微信公眾號-「SelfImprovementLab」
知乎:https://zhuanlan.zhihu.com/c_147249273
CSDN:http://blog.csdn.net/JUNJUN_ZHAO/article/details/78928182
Vectorization 向量化
(字幕來源:網易云課堂)
Welcome back. Vectorization is basically the art of getting rid of explicit for loops in your code.In the deep learning era safety in deep learning in practice,you often find yourself training on relatively large data sets,because that’s when deep learning algorithms tend to shine.And so, it’s important that your code very quickly because otherwise,if it’s running on a big data set,your code might take a long time to run,then you just find yourself waiting a very long time to get the result.
歡迎回來,向量化通常是消除你的代碼中顯式 for 循環語句的藝術。在深度學習安全領域、深度學習、練習中,你經常發現在訓練大數據集時,深度學習算法表現才更加優越,所以你的代碼運行得非常快非常重要。否則,如果它運行在一個大的數據集上面,你的代碼可能花費很長時間去運行,你會發現你將要等待非常長的時間去得到結果。
So in the deep learning era.I think the ability to perform vectorization has become a key skill.Let’s start with an example.So, what is Vectorization?In logistic regression you need to compute z equals W transpose X plus B,where W was this column vector and X is also this vector.Maybe there are very large vectors if you have a lot of features.So, w and x were both these RnX dimensional vectors.So, to compute W transpose X,if you had a non-vectorized implementation,you would do something like z equals zero.And then for I in range of n-X.So, for i equals 1, to n_x,z+=w[i]*x[i]And then maybe you do z+=b at the end.So, that’s a non-vectorized implementation.
所以在深度學習領域,我認為可以去完成向量化以及變成一個關鍵的技巧,讓我們用一個例子開始,什么是向量化?,在 Logistic 回歸中,你需要去計算 for i in range(n_x),python代碼 for i in range(n_x),然后z+=w[i]*x[i],最后z+=b,所以 這是一個非向量化的實現。
Then you find that that’s going to be really slow.In contrast, a vectorized implementation would just compute W transpose X directly.In Python or a numpy,the command you use for that is z=np.dot(w,x) so this computes w transpose x.And you can also just add b to that directly.And you find that this is much faster.Let’s actually illustrate this with a little demo.So, here’s my jupyter notebook in which I’m going to write some Python code.
你會發現這是真的很慢,作為對比 一個向量化的實現,將會非常直接計算 z=np.dot(w,x),這是在計算
So, first, let me import the numpy library to import.Send np. And so, for example,I can create A as an array as follows.Let’s say print A.Now, having written this chunk of code,if I hit shift enter,then it executes the code.So, it created the array A and it prints it out.Now, let’s do the Vectorization demo.I’m going to import the time libraries, since we use that,in order to time how long different operations take.
首先 讓我們導入numpy庫,作為 np 例如,像下面這樣我將要創建一個數組 A,讓我們看下 print A,現在 寫下這些代碼塊,如果我在鍵盤敲擊 shift 和 enter 兩個鍵,它將要執行這個代碼,所以 它創建了數組 A 以及 print 它,現在 讓我們完成向量化的例子,我將要導入time 庫 因為我要使用那個,為了去計算兩次不同的操作花費了多長時間。
Can they create an array A?Those random thought rand.This creates a million dimensional array with random values. b = np.random.rand.Another million dimensional array.And, now, tic=time.time, so this measure the current time,c = np.dot (a, b).toc = time.time.And this print,it is the vectorized version.
它們能創建一個數組 A 嗎,通過rand函數隨機得到,用隨機值創建了一個百萬維度的數組,b 等于 np.random.rand.,另外一個百萬維度的數組,現在 tic=time.time 記錄一下當前時間,c 等于 np.dot (a, b).,toc 等于 time.time. print一下,向量化的版本。
import numpy as np
# 2.11 Vectorization| 向量化 --Andrew Ng
a = np.array([1,2,3,4,5])
print(a)
# [1 2 3 4 5]
# [Finished in 0.3s]
import time
# 隨機創建 百萬維度的數組 1000000 個數據
a = np.random.rand(1000000)
b = np.random.rand(1000000)
# 記錄當前時間
tic = time.time()
# 執行計算代碼 2 個數組相乘
c = np.dot(a,b)
# 再次記錄時間
toc = time.time()
# str(1000*(toc-tic)) 計算運行之間 * 1000 毫秒級
print('Vectorization vresion:',str(1000*(toc-tic)),' ms')
print(c)
# Vectorization vresion: 6.009101867675781 ms
# [Finished in 1.1s]
c = 0
tic = time.time()
for i in range(1000000):
c += a[i]*b[i]
toc = time.time()
print(c)
print('For loop :',str(1000*(toc-tic)),' ms')
# For loop : 588.9410972595215 ms
# c= 249960.353586
# NOTE: It is obvious that the for loop method is too slowIt’s a vectorize version.And so, let’s print out.Let’s see the last time,so there’s toc - tic x 1000,so that we can express this in milliseconds.So, ms is milliseconds.I’m going to hit Shift Enter.So, that code took about three milliseconds or this time 1.5,maybe about 1.5 or 3.5 milliseconds at a time.It varies a little bit as I run it,but looks like maybe on average it’s taking like 1.5 milliseconds,maybe two milliseconds as I run this.All right.
這是一個向量化的版本,現在讓我們 print 一下,讓我們看一下運行時間,這是 ·toc - tic x 1000·,所以我們表達這個在毫秒級上,ms 代表毫秒,我將要同時敲擊 Shift 和 Enter,所以這個代碼花費 3 毫秒或者這個時間的 1.5 倍,或許大概 1.5 或者 3.5 毫秒,它有點變化當我再次運行它的時候,但是好像 平均她要花費 1.5 毫秒,或許我這次運行是 2 毫秒,是的。
Let’s keep adding to this block of code.That’s not implementing non-vectorize version.Let’s see, c = 0,tic = time.time.Now, let’s implement a for loop.For I in range of 1 million,I’ll pick out the number of zeros right.C += (a,i) x (b,i),and then toc = time.time.Finally, print more than explicit for loop.The time it takes is this 1000 x toc - tic + “ms” to know that we’re doing this in milliseconds.
讓我們繼續增加這個代碼,這是非向量化的版本,讓我們看看 c=0,then tic = time.time.,現在它實現了一個for 循環,python 代碼:for i in range 1:1000000,我將要取出 0 右邊的數字,而 C += (a,i) x (b,i),以及 toc = time.time.,最后 print for loop,它花費的時間是1000*toc-tic ms,為了知道我們正在做這個在毫秒級別。
Let’s do one more thing.Let’s just print out the value of C. we compute it to make sure that it’s the same value in both cases.I’m going to hit shift enter to run this and check that out.In both cases, the vectorize version and the non-vectorize version computed the same values,as you know, 2.50 to 6.99, so on.The vectorize version took 1.5 milliseconds. The explicit for loop and non-vectorize version took about 400, almost 500 milliseconds.The non-vectorize version took something like 300 times longer than the vectorize version.
讓我們再做點其他的事情,我們 print 出 C 的值。,計算一下它確認在兩個案例中他們是相同的。我打算去敲擊 shift 和 enter 去運行這個 檢查一下結果,在兩個案例中 向量化版本,和非向量化版本計算了相同的值,正如你知道的 2.50 到 6.99,向量化版本花費了 1.5 毫秒,很明確 for loop 和非向量化版本,花費了大約 400 幾乎 500毫秒,非向量化版本多花費了,300 倍向量化版本的時間。
With this example you see that if only you remember to vectorize your code,your code actually runs over 300 times faster.Let’s just run it again.Just run it again.Yeah. Vectorize version 1.5 milliseconds seconds and the for loop.So 481 milliseconds, again,about 300 times slower to do the explicit for loop.If the time slows down,it’s the difference between your code taking maybe one minute to run versus taking say five hours to run.
用這個例子你將會看見,如果你僅僅記住去向量化你的代碼,你的代碼完全運行 300 倍快,讓我們再次運行一下它,再次運行一下它,向量化版本 1.5 毫秒 循環使用了,481 毫秒,大約慢 300 倍用循環做這個,如果時間變慢,如果你的代碼一分鐘就出結果,那和 5 個小時出結果相差太遠了。
And when you are implementing deep learning algorithms,you can really get a result back faster.It will be much faster if you vectorize your code.Some of you might have heard that a lot of scaleable deep learning implementations are done on a GPU or a graphics processing unit.But all the demos I did just now in the jupyter notebook where actually on the CPU.
當你正在實現深度學習算法,這樣真的可以更快得到結果,向量化之后 運行速度會大幅上升,你可能聽過很多這樣的話,可擴展深度學習實現是在 GPU上 做的,GPU 也叫圖像處理單元,但是我做的所有的案例都是在 jupyter notebook上面實現,這里只有 CPU。
And it turns out that both GPU and CPU have parallelization instructions.They’re sometimes called SIMD instructions.This stands for a single instruction multiple data.But what this basically means is that,if you use built-in functions such as this np.function or other functions that don’t require you explicitly implementing a for loop.,It enables Python numpy to take much better advantage of parallelism,to do your computations much faster.And this is true both computations on CPUs and computations on GPUs.
CPU 和 GPU,都有并行化的指令,有時候會叫做SIMD指令,意思是單指令流多數據流,這個詞的意思是,如果你使用了這樣的內置函數,np.function 或者,其他能讓你去掉顯式for循環的函數,這樣 python 的numpy 能夠充分利用并行化,去更快的計算,這點對 GPU 和 CPU上面計算都是成立的。
It’s just that GPUs are remarkably good at these SIMD calculations ,but CPU is actually also not too bad at that. ,Maybe just not as good as GPUs.,You’re seeing how vectorization can significantly speed up your code.The rule of thumb to remember is whenever possible, avoid using explicit four loops.,Let’s go onto the next video ,to see some more examples of vectorization,and also start to vectorize logistic regression.
GPU 更加擅長 SIMD 計算,但是 CPU 事實上也不是太差,可能沒有 GPU 那么擅長吧,你們見到了向量化能夠加速你的代碼,經驗法則是 只要有其他可能 就不要使用顯式 for 循環,讓我們進入到下一個視頻,去看下更多的向量化的案例,開始向量化 Logistic 回歸。
重點總結:
向量化(Vectorization)
在深度學習的算法中,我們通常擁有大量的數據,在程序的編寫過程中,應該盡最大可能的少使用 loop 循環語句,利用 python 可以實現矩陣運算,進而來提高程序的運行速度,避免 for 循環的使用。
邏輯回歸向量化
- 輸入矩陣
X :(nx,m) - 權重矩陣
w :(nx,1) - 偏置
b :為一個常數 - 輸出矩陣
Y :(1,m)
所有 m 個樣本的線性輸出 Z 可以用矩陣表示:
Z = np.dot(w.T,X) + b
A = sigmoid(Z)參考文獻:
[1]. 大樹先生.吳恩達Coursera深度學習課程 DeepLearning.ai 提煉筆記(1-2)– 神經網絡基礎
PS: 歡迎掃碼關注公眾號:「SelfImprovementLab」!專注「深度學習」,「機器學習」,「人工智能」。以及 「早起」,「閱讀」,「運動」,「英語 」「其他」不定期建群 打卡互助活動。

智能推薦
Coursera | Andrew Ng (02-week-1-1.11)—神經網絡的權重初始化
該系列僅在原課程基礎上部分知識點添加個人學習筆記,或相關推導補充等。如有錯誤,還請批評指教。在學習了 Andrew Ng 課程的基礎上,為了更方便的查閱復習,將其整理成文字。因本人一直在學習英語,所以該系列以英文為主,同時也建議讀者以英文為主,中文輔助,以便后期進階時,為學習相關領域的學術論文做鋪墊。- ZJ Coursera 課程 |deeplearning.ai |網易云課堂 轉載請注明作者和...
Coursera | Andrew Ng (02-week-1-1.6)—Dropout 正則化
該系列僅在原課程基礎上部分知識點添加個人學習筆記,或相關推導補充等。如有錯誤,還請批評指教。在學習了 Andrew Ng 課程的基礎上,為了更方便的查閱復習,將其整理成文字。因本人一直在學習英語,所以該系列以英文為主,同時也建議讀者以英文為主,中文輔助,以便后期進階時,為學習相關領域的學術論文做鋪墊。- ZJ Coursera 課程 |deeplearning.ai |網易云課堂 轉載請注明作者和...
Coursera | Andrew Ng (02-week3-3.2)—為超參數選擇合適的范圍
該系列僅在原課程基礎上部分知識點添加個人學習筆記,或相關推導補充等。如有錯誤,還請批評指教。在學習了 Andrew Ng 課程的基礎上,為了更方便的查閱復習,將其整理成文字。因本人一直在學習英語,所以該系列以英文為主,同時也建議讀者以英文為主,中文輔助,以便后期進階時,為學習相關領域的學術論文做鋪墊。- ZJ Coursera 課程 |deeplearning.ai |網易云課堂 轉載請注明作者和...
Coursera | Andrew Ng (04-week1)—卷積神經網絡
在吳恩達深度學習視頻以及大樹先生的博客提煉筆記基礎上添加個人理解,原大樹先生博客可查看該鏈接地址大樹先生的博客- ZJ Coursera 課程 |deeplearning.ai |網易云課堂 CSDN:http://blog.csdn.net/junjun_zhao/article/details/79190634 Convolutional Neural Networks (卷積神經網絡) We...
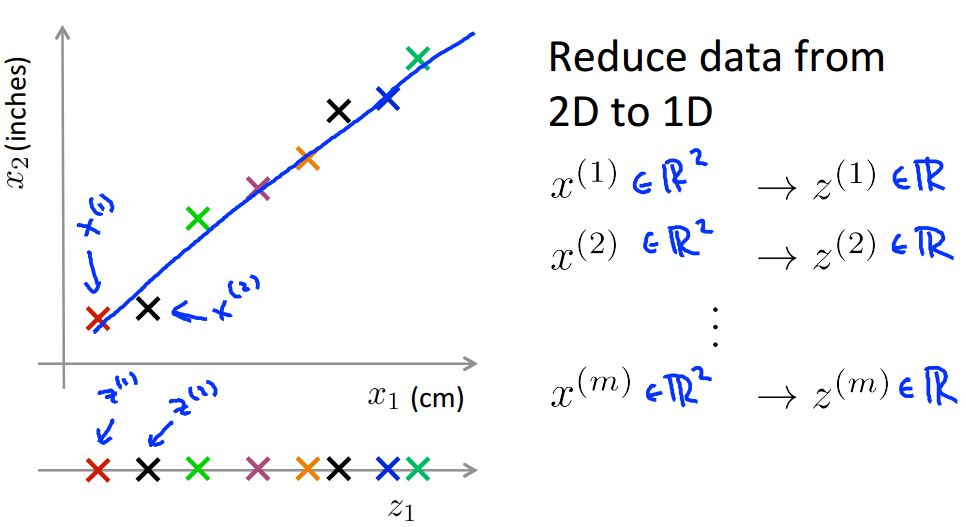
Coursera 機器學習(by Andrew Ng)課程學習筆記 Week 8(二)——降維
此系列為 Coursera 網站機器學習課程個人學習筆記(僅供參考) 課程網址:https://www.coursera.org/learn/machine-learning 參考資料:http://blog.csdn.net/MajorDong100/article/details/51104784 一、降維的作用 1.1 數據壓縮 數據壓縮(Data Compression)不僅能減少數據的存...
猜你喜歡
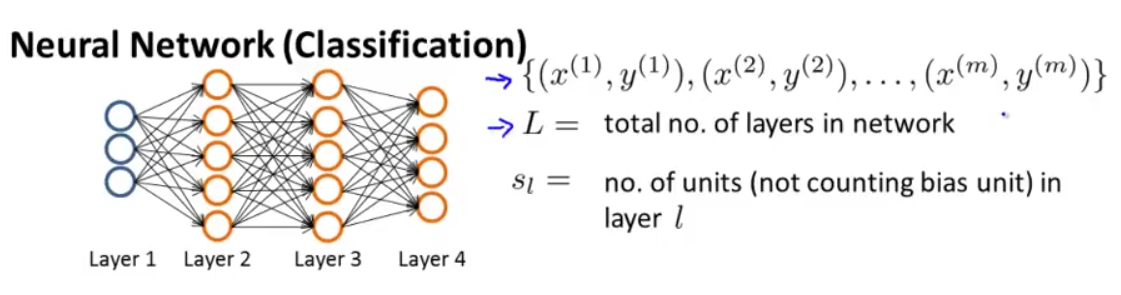
Coursera 機器學習(by Andrew Ng)課程學習筆記 Week 5——神經網絡(二)
此系列為 Coursera 網站機器學習課程個人學習筆記(僅供參考) 課程網址:https://www.coursera.org/learn/machine-learning 參考資料:http://blog.csdn.net/SCUT_Arucee/article/details/50176159 一、神經網絡的代價函數 1.1 神經網絡的模型參數 假設我們有下圖這樣的神經網絡: 我們定義以下符...
Andrew Ng coursera上的《機器學習》ex4
Andrew Ng coursera上的《機器學習》ex4 按照課程所給的ex4的文檔要求,ex4要求完成以下幾個計算過程的代碼編寫: exerciseName description sigmoidGradient.m compute the grident of the sigmoid function randInitializedWeights.m randomly initialize ...
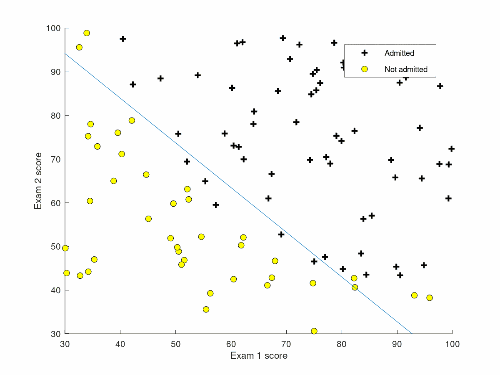
Ex02 [coursera] Machine learning - Stanford University - Andrew Ng
Logistic Regression 目錄 Part1 ex2.m plotData.m sigmoid.m costFunction.m plotDecisionBoundary.m predict.m prompt output figure output Part2 ex2_reg.m mapFeature.m costFunctionReg.m prompt output ...
Outline of Machine Learning created by Andrew Ng on Coursera
By the time you finish this class * You’ll know how to apply the most advanced machine learning algorithms to such problems as anti-spam, image recognition, clustering, building recommender syst...
ML - Coursera Andrew Ng - Week1 & Week2 & Ex1 - Linear Regression - 筆記與代碼
Week 1和Week 2主要講解了機器學習中的一些基礎概念,并介紹了線性回歸算法(Linear Regression)。 機器學習主要分為三類: 監督學習(Supervised Learning):已知給定輸入的數據集的輸出結果。監督學習是學習輸入和輸出之間的映射關系。根據輸出值的類型監督學習問題可分為回歸(regression)問題和分類(classification)問題。如果輸出值是連續的...